15-18. Verdadeiro/Falso. Suponha que seja contínua em toda parte. Determine se a afirmação dada é verdadeira ou falsa. Explique sua resposta.

16. Se tiver um máximo relativo em , então será um ponto crítico de .

Então galera, essa afirmativa aqui vem do famoso Teorema de Fermat, que diz que:

Se é um ponto de máximo ou mínimo relativo, então . Em outras palavras, se tem um máximo relativo em , NECESSARIAMENTE a derivada tem que ser nula nesse ponto, uma vez que a mesma é horizontal para esse valor de . A recíproca do Teorema de Fermat não é verdadeira, pode existir pontos em que a derivada se anula, mas que não são pontos de máximo ou mínimo. A função é um bom exemplo, se liga:

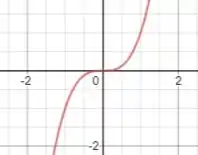
Note que em a derivada é nula, mas não é um ponto de máximo ou mínimo. Sendo assim, podemos concluir que a afirmativa é verdadeira.