Enunciado

Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 3.4 - Ex. 17g

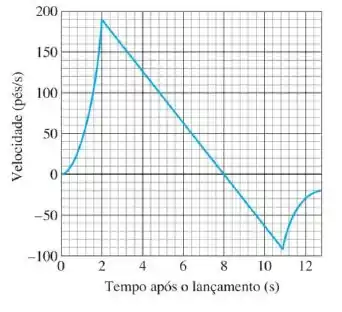
17. Lançamento de um foguete Quando um foguete em miniatura é lançado, os propulsores queimam combustível por alguns segundos, acelerando o foguete para cima. Terminada a combustão, o foguete ainda sobe um pouco e depois começa a cair. Em seguida, uma pequena carga de explosivos abre um paraquedas, que diminui a velocidade do foguete, impedindo que ele seja danificado durante o pouso. A figura a seguir mostra os dados de velocidade da trajetória de um foguete em miniatura. Use-os para responder às seguintes

questões:

f. Quando sua aceleração se tornou constante? Qual era seu valor ( o inteiro mais próximo)?

Passo 1

Para a aceleração ser constante, sua velocidade deve ser linear, pois, se derivarmos uma função do primeiro grau obteremos uma constante:

A variação da velocidade é linear, ou seja, a aceleração é constante, do momento em que o motor para de funcionar, , até quando o paraquedas abre, .

Portanto sua aceleração será:

Resposta

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O topo de uma escada desliza, por uma parede vertical a uma taxa de 0,15 m s . No momento em que a base da escada está a 3 m da parede, ela afasta-se da parede à velocidade de 0,2 m s . Qual o comprim

Suponha 4 x 2 + 9 y 2 = 36 , onde x e y são funções de t. (a) Se , (a) Se d y / d t = 1 3 , encontre d x / d t quando x = 2 e y = 2 3 5 . (b) Se d x / d t = 3 , encontre d y / d t quando x = - 2 e y =

Uma partícula move-se ao longo da curva y = 2s e n( π x / 2 ) . Quando a partícula passa pelo ponto ( 1 3 , 1 ) , sua coordenada x cresce a uma taxa de 10c m / s . Quão rápido a distância da partícula

Se x 2 + y 2 + z 2 = 9 , d x / d t = 5 e d y / d t = 4 , encontre d z / d t quando x , y , z = ( 2,2 , 1 ) .

Uma torneira está preenchendo uma pia hemisférica de 60c m de diâmetro com água a uma taxa de 2 L m i n . Encontre a taxa na qual a água está aumentando na pia quando estiver cheia até a metade. [Use