O topo de uma escada desliza, por uma parede vertical a uma taxa de . No momento em que a base da escada está a da parede, ela afasta-se da parede à velocidade de . Qual o comprimento da escada ?
Passo 1
Eaee, belezinha?? Bom... a questão nos diz que uma escada desliza a uma taxa de por uma parede vertical. No momento em que a base da escada está a da parede, ela afasta-se da parede à velocidade de .
Queremos calcular o comprimento da escada.
Primeiramente, através do enunciado podemos esboçar o seguinte esquema:
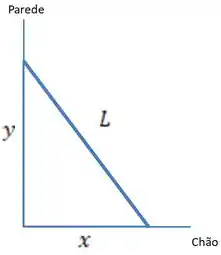
Agora vamos prosseguir!
Passo 2
Feito o esquema, podemos ver mais claramente a relação entre as variáveis do problema. No caso, por Pitágoras temos:
Onde é a posição da “base”, é a posição do “topo” da escada e é o comprimento da mesma.
Além disso, o enunciado estabelece as taxas de variação de e no tempo, ou seja:
Onde o sinal negativo se dá devido ao fato de diminuir conforme o tempo passa.
Passo 3
Para relacionar os dados do problema com a relação que encontramos no passo 2, derivamos implicitamente em relação à :
Passo 4
O enunciado nos informou que a taxa com que varia é de no instante em que .
Assim, substituindo os valores na expressão que encontramos no passo 3 podemos encontrar :
Ou seja, voltando à expressão do passo 2 temos:
Entendeu direitinho?? Responde aee 😉
Resposta
O comprimento da escada é de .