Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 3.9 - Ex. 22
Um bote é puxado em direção ao ancoradouro por uma corda que está atada na proa do bote e que passa por uma polia sobre o ancoradouro (colocada m mais alto que a proa). Se a corda for puxada a uma taxa de m/s, quão rápido se aproxima o bote do ancoradouro quando ele estiver a m dele?
Passo 1
Para entendermos o problema, devemos visualizar bem o que é proposto. Se chamarmos o comprimento da corda entre a proa do bote e a polia do ancoradouro de e a distância do barco ao ancoradouro de , temos a seguinte situação:
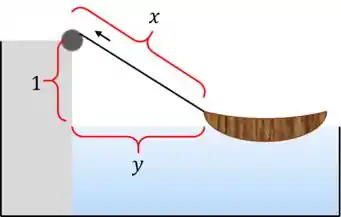
O que iremos fazer nessa atividade é equacionar o problema visto acima, e utilizarmos nossos conhecimentos de calculo, principalmente de derivadas como taxa de variação, para resolvermos essa atividade.
Passo 2
Como a situação descreve um triângulo retângulo, então, a relação pode ser feita por Pitágoras:
Derivando implicitamente em função do tempo () temos:
Passo 3
Se a corda for puxada a uma taxa de m/s, o comprimento da corda entre a proa do bote está decrescendo nessa mesma taxa, então , e quando o bote estiver a metro do ancoradouro () então o valor de é:
Agora é só substituir na derivada:
Então a distância do barco ao ancoradouro decresce (por causa do sinal negativo) a uma taxa de m/s.
Resposta
A distância do barco ao ancoradouro decresce a uma taxa de m/s.