Enunciado

Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 3.9 - Ex. 46

Uma roda-gigante com raio de está girando a uma taxa de uma revolução a cada dois minutos. Quão rápido um passageiro estará subindo quando seu assento estiver acima do nível do solo?

Passo 1

Opa, bora resolver essa questão!

O enunciado da pra a gente o seguinte problema: Uma roda-gigante com raio de está girando a uma taxa de uma revolução a cada dois minutos e ele pergunta pra a gente a velocidade que uma passageiro a de altura!

Bora desenhar um esqueminha:

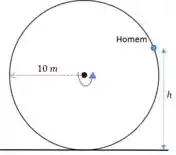
Aqui a gente tem a informação da taxa de revolução da roda gigante, ou seja, sua velocidade angular:

E queremos:

Passo 2

Agora vamos olhar a roda gigante com mais cuidado e tentar tirar algumas relações:

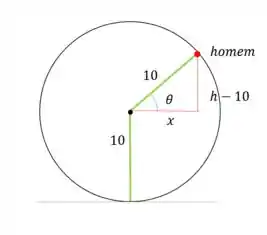
Podemos utilizar pitágoras pra fazer:

Sabemos que a :

Agora podemos relacionar com , fazendo:

Passo 3

Agora podemos derivar:

Usando a regra da cadeia:

Temos:

Então:

Prontinhooo!

Resposta

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Seja x = f t ,t ≥ 0 ,t a lq u e f 0 = 1 e f 1 = 2 . Suponha, ainda, que d x d t0 para t ≥ 0 ; d 2 x d t 20 para 0t1 e d 2 x d t 20 para t1 . Como você acha que deve ser o gráfico de f ? Porquê?

Enche-se um reservatório, cuja forma é a de um cone circular reto, de água a uma taxa de 0,1 m³/s. O vértice está a 15 m do topo e o raio do topo é de 10 m. Com que velocidade o nível h da água e

Uma escada de 8m está encostada em uma parede. Se a extremidade inferior da escada for afastada do pé́ da parede a uma velocidade constante de 2 (m/s), com que velocidade a extremidade superior estar

Dois pontos P e Q deslocam-se, respectivamente, nos eixos x e y de modo que a soma das distâncias de P a R e de R a Q mantém-se constante e igual a e durante o movimento, em que R = 0 , h é um ponto

Seja f t = t 3 + 3 t 2 .a) Estude o sinal de f ' t .b) Estude o sinal de f ' ' t .c) Calcule lim t → + ∞ ⁡ t 3 + 3 t 2 e lim t → - ∞ ⁡ t 3 + 3 t 2 .d) Utilizando as informações acima, esboce o gráfico