Enunciado
Cálculo - Diva Flemming - Cálculo A- Ed: 6º - Capítulo 4.7 - Ex. 14
Quantas retas tangentes à curva passam pelo ponto ? Em quais pontos essas retas tangentes tocam a curva?
Passo 1
O gráfico a seguir mostra uma simulação na qual podemos observar duas retas tangentes que passam por .
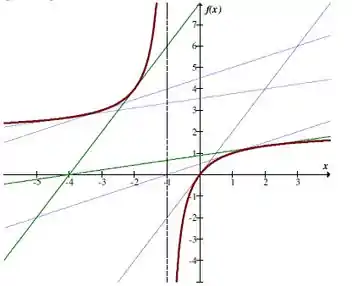
Para encontrar o ponto de tangência temos:
Vamos supor o ponto de tangência. A equação da reta tangente é: .
Substituindo o ponto :
Precisamos encontrar . No ponto de tangência:
Assim, temos:
Passo 2
Resolvendo essa igualdade temos:
Uma vez que temos o valor de , vamos descobrir o valor de :
Assim, os pontos de tangência são:
As equações das retas tangentes são iguais a:
Resposta
Os pontos de tangência são:
Exercícios de Livros Relacionados
Nos Exercícios de 43 a 46, ache f ' ( a ) aplicando a fórmula (4).46) f x = 2 x - 1 ; a = 4
Nos Exercícios de 31 a 38, ache a derivada indicada.37) D x 1 x 2 - x
Nos Exercícios de 51 a 56, ache d y d x .51)y = 4 x 2 + 3 x
Nos Exercícios de 43 a 46, ache f ' ( a ) aplicando a fórmula (4).43) f x = 4 - x 2 ; a = 5
Nos Exercícios de 47 a 50, ache f ' ( a ) aplicando a fórmula (7).49) f x = 1 2 x + 3 ; a = 3