Enunciado
Cálculo - Diva Flemming - Cálculo A- Ed: 6º - Capítulo 4.7 - Ex. 11
Dada a função , verificar se existe . Esboçar o gráfico.
Passo 1
Vamos ver se é contínua, para saber se existe
Vamos ver o que é necessário para uma função ser contínua no ponto :
- é definida no ponto ;
- existe;
- .
Vamos então ver se as três condições são aceitas.
Passo 2
Primeiro vamos ver se é definida no ponto :
A função nos diz que:
Eita, ela não é definida nesse ponto, assim não existe .
Passo 3
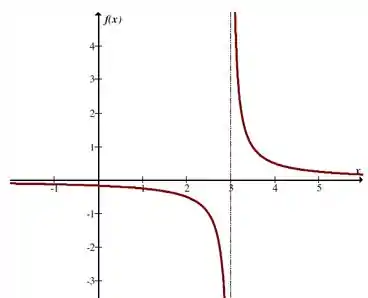
Vamos esboçar o gráfico:
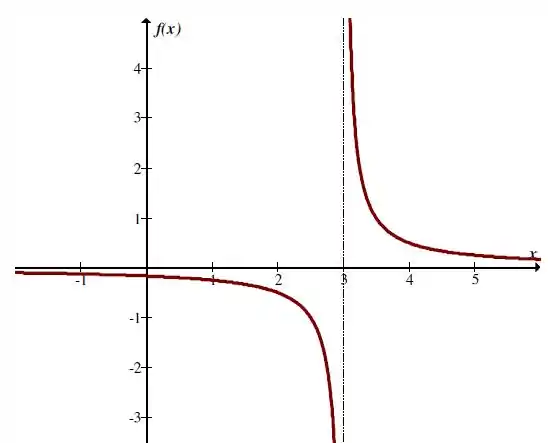
Resposta
Não existe
Exercícios de Livros Relacionados
Nos Exercícios de 51 a 56, ache d y d x .53)y = 2 - 7 x
Nos Exercícios de 31 a 38, ache a derivada indicada.34) D x ( 1 x + 1 )
57) Se g é contínua em a e f x = x - a . g x , ache f ' ( a ) . (Sugestão: use a fórmula (7)).
Nos Exercícios de 51 a 56, ache d y d x .52)y = 4 2 x - 5
Nos Exercícios de 47 a 50, ache f ' ( a ) aplicando a fórmula (7).47) f x = 2 - x 3 ; a = - 2