Enunciado
Cálculo - Diva Flemming - Cálculo A- Ed: 6º - Capítulo 4.7 - Ex. 10
Dada a função , verificar se existe . Esboçar o gráfico.
Passo 1
Vamos ver se é contínua, para saber se existe
Vamos ver o que é necessário para uma função ser contínua no ponto :
- é definida no ponto ;
- existe;
- .
Vamos então ver se as três condições são aceitas.
Passo 2
Primeiro vamos ver se é definida no ponto :
A função nos diz que:
Então ela é definida nesse ponto.
Passo 3
Vamos agora ver se o existe, para isso valor calcular esse limite pela direita e pela esquerda, se eles forem iguais, o limite existe e possui esse valor:
Eita, não existe, não passa pela segunda condição, assim não existe .
Passo 4
Vamos esboçar o gráfico:
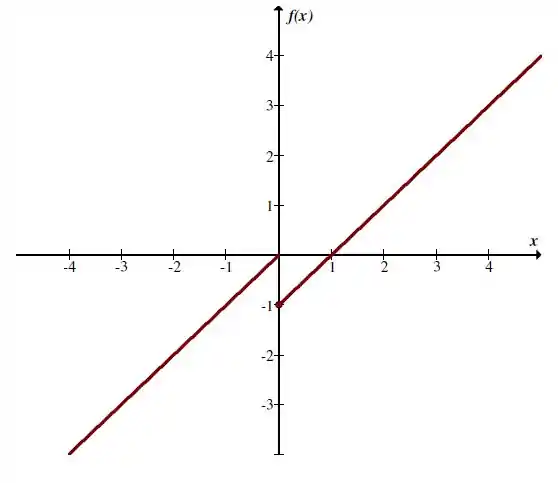
Resposta
Não existe
Exercícios de Livros Relacionados
Nos Exercícios de 31 a 38, ache a derivada indicada.38) D x 3 1 + x 2
Nos Exercícios de 47 a 50, ache f ' ( a ) aplicando a fórmula (7).48) f x = x 2 - x + 4 ; a = 4
Nos Exercícios de 51 a 56, ache d y d x .54)y = 1 x - 1
58) Se g é contínua em a e f x = x 2 - a 2 . g x , ache f ' ( a ) . (Sugestão: use a fórmula (7)).
Nos Exercícios de 51 a 56, ache d y d x .55)y = x 3