Enunciado

Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 0.Revisão - Ex. 21

21. Suponha que a temperatura mínima esperada em Anchorage, no Alasca (em F°), seja modelada pela equação

Onde está em dias e corresponde a 1° de janeiro.

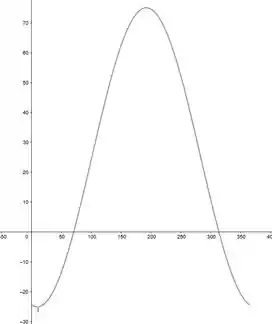
Esboce o gráfico de para

Use o modelo para prever quando ocorrerá o dia mais frio do ano.

Com base no modelo, quantos dias durante o ano se espera ter uma temperatura abaixo de .

Passo 1

Show de bolinhas meus amores, usando uma ferramente gráfica, podemos esboçar o gráfico de:

Ele é dado por:

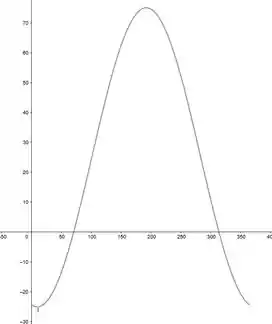
Passo 2

Logo, o dia mais frio do ano vai acontecer quando o gráfico tiver seu valor mínimo, ou seja, no ponto P dado em:

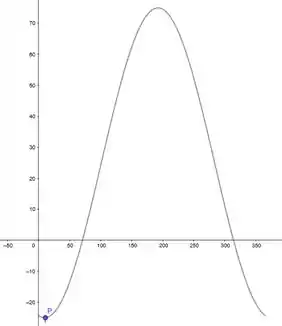
E estimando esse valor, chegamos a aproximadamente 11 dias. E de acordo com o calendário, 11 dias após começar o ano, estamo em 11 de janeiro.

Passo 3

E agora, na letra (c), queremos estimar quantos dias a temperatura será menor que F, isso acontece com todos os dias que estão abaixo do eixo y (linha vermelha), tal que:

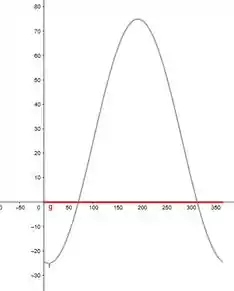
Esses dias vão ser esse pintados:

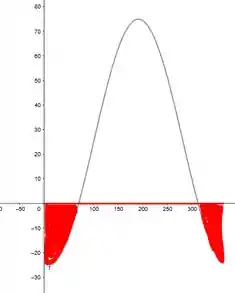
Logo, podemos estimar que para a primeira parte, fomos até mais ou menos o dia 70 e poucos, vamos aproximar para 76 dias. E a segunda parte, temos um pouco menos, por que saímos do dia 320 e poucos e vamos até o dia 365, ou seja, uma diferença de cerca de 45 dias, bora aproximar para 46 dias. Logo, os dias totais são:

Portanto, a temperatura é abaixo de em cerca de 122 dias do ano.

Resposta

11 de janeiro.
122 dias.

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Use a periodicidade das funções tangente e cotangente, bem como os valores do t g t , e c o t g ( t ) , quando 0 ≤ tπ , para determinar o valor exato da função c o t g - 1 6 π .

Use a periodicidade das funções tangente e cotangente, bem como os valores do t g t , e c o t g ( t ) , quando 0 ≤ tπ , para determinar o valor exato da função t g 4 3 π .

Use a periodicidade das funções tangente e cotangente, bem como os valores do t g t , e c o t g ( t ) , quando 0 ≤ tπ , para determinar o valor exato da função c o t g 11 3 π .

Encontre todos os valores de t no intervalo [ 0,2 π ) em que a equação t gt = -1 está satisfeita.

Use a periodicidade das funções tangente e cotangente, bem como os valores do t g t , e c o t g ( t ) , quando 0 ≤ tπ , para determinar o valor exato da função c o t g - 11 4 π .