Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 1 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 4.8 - Ex. 21

21. Use o método de Newton para encontrar todas as raízes da equação com precisão de seis casas decimais.

cos ⁡ x = x

Passo 1

Faala ae, eu sou o Rafha do Responde Aí e vou te ajudar nessa questão!

Nossa equação é a seguinte:

cos ⁡ x = x

E queremos encontrar a sua raiz, isso é, o valor de x para o qual:

cos ⁡ x - x = 0

De forma que nossa função a qual queremos encontrar a raíz é portanto:

f x = cos ⁡ x - x

E queremos encontrar todas as suas raízes.

Para isso vamos usar um método iterativo que é o método de Newton.

Basicamente, nós começamos com um chute inicial para essa raiz.

x 1

E para encontrar o próximo valor, faremos a seguinte iteração:

x n + 1 = x n - f ( x n ) f ' ( x n )

O enunciado pede para encontrarmos com uma precisão de seis casas decimais, dessa forma, teremos que ir realizando iterações até que o valor encontrado não se altere até a sexta casa decimal.Dá trabalho? Dá... mas a vida é uma sopa e você tá de garfo :0

Passo 2

No nosso método iterativo, temos que:

x n + 1 = x n - f ( x n ) f ' ( x n )

Dessa forma, precisamos da derivada de

f x = cos ⁡ x - x

Que pode ser reescrita para facilitar a derivação:

f x = cos ⁡ x - x 1 2

Derivando, teremos:

f ' x = - s e n x - 1 2 x 1 2 - 1

f ' x = - s e n x - 1 2 x - 1 / 2

f ' x = - s e n x - 1 2 x

Passo 3

Pronto, agora que temos f ' x é só jogar na fórmula de Newton:

x n + 1 = x n - f x n f ' x n

x n + 1 = x n - cos ⁡ x n - x n - s e n x n - 1 2 x n

Vamos agora analisar qual valor usar para x 1 .

Para isso, podemos usar a seguinte estratégia. Queremos que:

cos ⁡ x - x = 0

Isso é o mesmo que:

cos ⁡ x = x

O gráfico do cosseno e o gráfico da raíz de x são conhecidos. Teoricamente, sabemos esboça-los.

Dessa forma, vamos esboçar ambos os gráficos e verificar em quais pontos eles se encontram, ou seja, em quais pontos cos ⁡ x = x

Esses são também pontos onde cos ⁡ x - x = 0 , que é o que queremos!

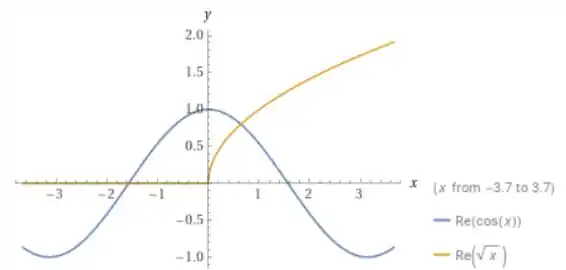
A função x só é definida para valores de x maiores ou iguais a zero, logo, só iremos considerar aqui valores de x que sejam

x > 0

Olhando no gráfico vemos que as curvas se interceptam em x próximo de 0,7 .

Dessa forma, esse será o nosso chute inicial.

x 1 = 0,7

Passo 4

Vamos usar que x 1 = 0,7 :

x n + 1 = x n - cos ⁡ x n - x n - s e n x n - 1 2 x n

Logo,

x 2 = 0,7 - cos ⁡ 0,7 - 0,7 - s e n 0,7 - 1 2 0,7

Fazendo as contas:

x 2 ≈ 0,642167

Para achar x 3 o processo é análogo. Logo,

x 2 = 0 , 642167 - cos ⁡ 0 , 642167 - 0 , 642167 - s e n 0 , 642167 - 1 2 0 , 642167

x 3 ≈ 0,641714

Para x 4 :

x 2 = 0 , 641714 - cos ⁡ 0 , 641714 - 0 , 641714 - s e n 0 , 641714 - 1 2 0 , 641714

x 4 ≈ 0,641714

Opa, como deu igual já podemos parar. Pois nos aproximamos o suficiente da raiz. Logo, a raiz aproximada de seis casas decimais será 0,641714

Resposta

A raiz aproximada de seis casas decimais será 0,641714

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

22) Calcule Δ y e d y para os valores dados de x e d x = Δ x . A seguir, esboce um diagrama como o da Figura 5, mostrando os segmentos de reta com comprimentos d x , d y e Δ y . y = e x , x = 0 , Δ x
19) Compute Δ y e d y para os valores dados de x e d x = Δ x . A seguir, esboce um diagrama como o da Figura 5, mostrando os segmentos de reta com comprimentos d x , d y e Δ y . y = 2 x - x 2 , x = 2
39) Se uma correnteI passar por um resistor com resistência R , a Lei de Ohm afirma que a queda de voltagem é V = R I . Se V for constante e R for medida com um certo erro, use diferenciais para mostr
30) Explique em termos de aproximações lineares ou de diferenciais por que a aproximação é razoável. 1,01 6 ≈ 1,06
36) Use as diferenciais para estimar a quantidade de tinta necessária para aplicar uma camada de 0,05c m de tinta a um domo com diâmetro de 50m .