Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 3.10 - Ex. 22
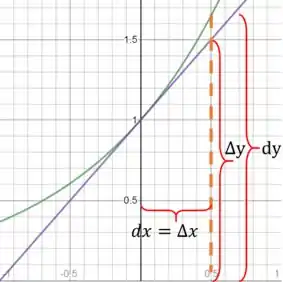
22) Calcule e para os valores dados de e . A seguir, esboce um diagrama como o da Figura 5, mostrando os segmentos de reta com comprimentos , e .
Passo 1
A diferencial de uma função é dada por: :
Portanto, derivando a função:
Logo, a diferencial é:
Então temos:
Passo 2
E como então:
Passo 3
Temos a reta tangente em :
Portanto temos o gráfico
Resposta
Exercícios de Livros Relacionados
Cada função f(x) varia quando x varia de x 0 para x 0 + d x . Determine :a variação Δ f = f x 0 + d x - f ( x 0 ) o valor da estimativa d f = f ' x 0 d x o erro de aproximação |Δ f - d f | f x =x - 1
Faça um esboço do gráfico e indique os seguimentos de reta cujos comprimentos são dy e ∆ y
Encontre dy e ∆ y para os valores de x e ∆ x . Sendo y = x²; x 0 = 2 ∆ x = 1
Nos exercícios de 31 a 34, faça o seguinte: (a) encontre d x e d y em termos de t e d t ; (b) use os resultados da parte (a) para encontrar d y d x ; (c) expresse y em termos de x , eliminando t , e e
Um tanque cilíndrico aberto, deve ter um revestimento externo com 2 cm de espessura. Se o raio interno for 6 m e a altura for 10 m, encontre, por diferenciais, a quantidade de material necessária para