Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 6.4 - Ex. 23

23. A densidade linear em qualquer ponto de uma barra com 3 m varia diretamente com a distância de um ponto a um ponto externo a ela, sobre a sua reta suporte e a 1 m de um extremo onde a densidade é 2 kg/m. Se a massa total da barra for 15 kg, ache o centro de massa da barra.

Passo 1

O primeiro passo para encontrar o centro de massa é achar a função da densidade dessa barra. Para isso vamos analisar a figura abaixo:

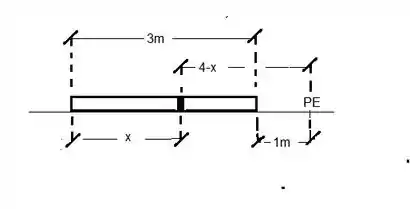
Pela figura percebemos que podemos escrever qualquer ponto, tendo como referencial o ponto externo, como ( 4 - x ) . Com isso estamos perto de achar uma função para densidade.

ρ x = k ( 4 - x )

Passo 2

Agora que conhecemos a cara da densidade, para que a função esteja completa precisamos achar o valor da constante k, para isso o exercício nos da a seguinte informação:

  1. A densidade no extremo é 2 kg/m, ou seja, ρ 3 = 2 .

Com essa informação podemos escrever da seguinte maneira:

2 = k ( 4 - 3 )

k = 2

Agora aplicamos k a função obtida no passo anterior:

ρ x = 2 4 - x

ρ x = 8 - 2 x

agora passamos ao próximo passo.

Passo 3

Para achar o centro de massa usaremos a seguinte relação:

x - = ∫ 0 l x ρ ( x ) M t

Onde l é o comprimento da barra e ρ ( x ) é a densidade.

Portanto temos a seguinte equação para o centro de massa:

x - = ∫ 0 3 x ( 8 - 2 x ) d x 15

x - = ∫ 0 3 ( 8 x - 2 x 2 ) d x 15

x - = 4 x 2 - 2 3 x 3 | 0 3 15

x - = 18 15 m

Resposta

Centro de massa: 18 15 m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Siga as instruções do Exercício 17 para os segmentos de curva y = x 8 3d ex = 10 - 3a t éx = 1 é e para o segmento y = x 3 8 de x = 10 - 8 até x = 1 .
Conforme a figura abaixo, uma viga horizontal com dimensões 2 pol × 6 pol × 16 pés (12 pol = 1 pé) fixada nos dois extremos é sujeita a uma carga uniformemente distribuída de 120 lb/pé. Como resultado
Suponha que nenhum segmento da curva x=x ( t ) ,y=y ( t ) ,( a≤t≤b ) seja percorrido mais de uma vez quando t cresce de a até b . Divida o intervalo [ a ,b ] em n subintervalos inserindo pontos t 1 ,t
Use um sistema de álgebra computacional ou uma tabela de integrais para indicar o comprimento exato do arco da curva y = e x que fica entre os pontos ( 0 ,1 ) e ( 2 , e 2 ) .
Ache o comprimento exato da curva. 36 y 2 = x 2 - 4 3 2 ≤ x ≤ 3 ,y ≥ 0