Conforme a figura abaixo, uma viga horizontal com dimensões 2 pol × 6 pol × 16 pés (12 pol = 1 pé) fixada nos dois extremos é sujeita a uma carga uniformemente distribuída de 120 lb/pé. Como resultado da carga, a linha central da viga sofre uma deflexão, que é descrita por:
onde é o comprimento da viga sem carga, é a distância horizontal ao longo da viga, medida em polegadas, a partir do extremo esquerdo, e é a deflexão da linha central em polegadas.
- Faça o gráfico de versus com .
- Encontre a deflação máxima da linha central.
- Use um CAS ou uma calculadora com integração numérica para encontrar o comprimento da linha central da viga carregada. Arredonde sua resposta para duas casas decimais.
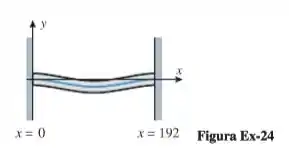
Passo 1
E aí, tudo joia?
Dá uma olhada no gráfico:
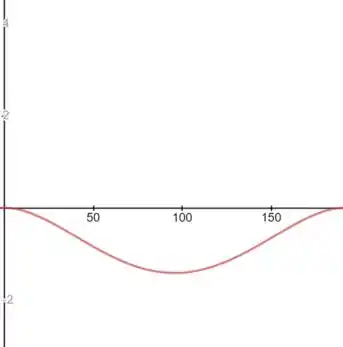
Esse aí é o gráfico, onde o eixo é a distância horizontal e é a deflação, no intervalo de .
Passo 2
b) Pelo gráfico e usando a calculadora do Desmos, vemos que a derivada é zero no ponto , esse é o ponto mínimo do gráfico, ou seja, onde ocorre a maior deflação.
A deflação máxima então é:
Passo 3
c) Pra calcular o comprimento da linha, vamos calcular a integral:
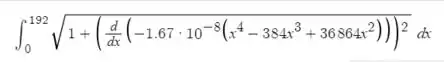
Usando o próprio Desmos pra calcular, com suas casas decimais temos que o comprimento é:
E prontinho! 😉
Resposta
- Gráfico.