Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 6.4 - Ex. 18

Siga as instruções do Exercício 17 para os segmentos de curva y = x 8 3   d e   x = 10 - 3   a t é   x = 1 e para o segmento y = x 3 8 de x = 10 - 8 até x = 1 .

Passo 1

E aí, tudo joia?

Vamos começar dando uma olhada nos gráficos? Vamos? Vamos.

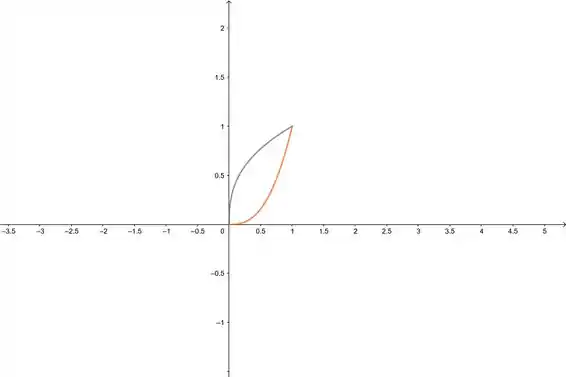
Pelo gráfico a gente vê que elas têm o mesmo comprimento, mas vamos calcular direitinho...

Passo 2

Vamos montar as expressões que determinam o comprimento das duas:

A gente pode chamar o primeiro comprimento de L 1 e o segundo de L 2 .

Vamos derivar a primeira:

y ' = 8 3 x 5 3

Aplicando na fórmula do comprimento então temos:

L 1 = ∫ 10 - 3 1 1 + 8 3 x 5 3 2   d x

L 1 = ∫ 10 - 3 1 1 + 64 9 x 10 3   d x  

=   ∫ 10 - 3 1 9 + 64 x 10 3 9   d x

= ∫ 10 - 3 1 9 + 64 x 10 3 3   d x

Passo 3

Agora vamos fazer o mesmo para a outra função:

y ' = 3 8 x - 5 8

L 2 = ∫ 10 - 8 1 1 + 3 8 x - 5 8 2   d x

L 2 = ∫ 10 - 8 1 1 + 9 64 x - 10 8   d x

= ∫ 10 - 8 1 64 x 10 8 + 9 64 x 10 8   d x  

= ∫ 10 - 8 1 64 10 8 + 9 8 x 5 8   d x

Passo 4

Temos que verificar que as duas são iguais. Pra isso, vamos fazer uma substituição na primeira e tentar chegar na segunda...

Vamos fazer u = x 8 3 → x = u 3 8 . E aí d x = 3 8 u - 5 8 .

Vamos substituir isso na primeira:

Primeiramente, os intervalos vão virar: 10 - 8   e   1 .

E a integral:

∫ 10 - 3 1 9 + 64 u 3 8 10 3 3     3 8 u - 5 8   d u

∫ 10 - 8 1 9 + 64 u 10 8 u 5 8   d u

Que é exatamente igual à outra integral, e com isso provamos que os comprimentos são iguais😉

Passo 5

Jogando essa integralzinha linda no Desmos a gente vai calcular um valor aproximado para o comprimento das curvas:

L = ∫ 10 - 3 1 9 + 64 x 10 3 3   d x

L ≈ 1,52 26

Prontinho! Esse é o comprimento aproximado das curvas😊

Resposta

L ≈ 1,5226

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Expresse o comprimento de arco exato da curva acima do intervalo dado como uma integral que tenha sido simplificada para eliminar o radical; em seguida, calcule a integral usando um CAS. y = ln ⁡ ( se
Na nossa definição de comprimento de arco do gráfico de y = f ( x ) , é necessário que f ' ( x ) seja uma função contínua para que f satisfaça as hipóteses do Teorema do Valor Médio (4.8.2)
A aproximação L ≈∑ k = 1 n 1 + f ' x k * 2Δ x k do comprimento de arco é exata quando f for uma função linear de x .
Encontre o comprimento de arco exato das curvas acima dos intervalos dados. y = ( x 6 + 8 ) / 16 x 2 ,d ex = 2a t éx = 3 é
Expresse o comprimento de arco exato da curva acima do intervalo dado como uma integral que tenha sido simplificada para eliminar o radical; em seguida, calcule a integral usando um CAS. y = ln ⁡ ( se