Enunciado
Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 6.4 - Ex. 19
Siga as instruções do Exercício 17 para os segmentos de curva e para o segmento de até .
Passo 1
E aí, tudo joia?
Vamos começar dando uma olhada nos gráficos:
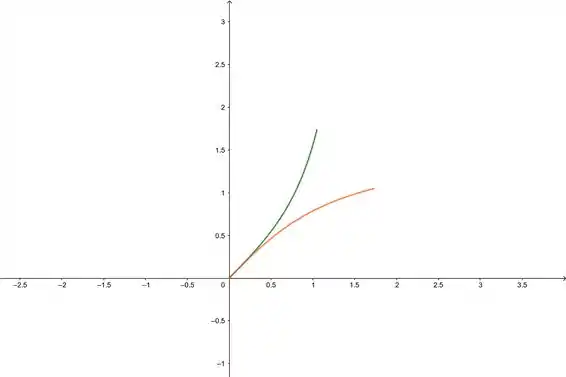
Belezinha! Aqui tá parecendo muito que são iguais né? Vamos ver isso...
Passo 2
Vamos montar as integrais de comprimento das duas. A primeira fica:
Beleza, vamos ver a segunda agora...
Passo 3
A segunda é:
Passo 4
Vamos agora mostrar que as duas integrais são iguais:
Vamos fazer na primeira a substituição:
Teremos: .
E aí os limites de integração viram: .
E como , teremos a integral:
Que é igualzinha a outra integral, só mudando a variável, ou seja, são iguais!
Passo 5
Vamos calcular o comprimento agora usando um programinha top pra calcular essa integral:
E pronto!
Resposta
Exercícios de Livros Relacionados
Use o Teorema de Pitágoras para encontrar o comprimento do segmento de reta de y = 5 x entre 0,0e( 1,5 ) e confirme que o valor está de acordo com o comprimento calculado usando:Fórmula (4)Fórmula (5)
Use o Teorema de Pitágoras para encontrar o comprimento do segmento de reta de y = 2 x entre 1,2 e( 2,4 ) e confirme que o valor está de acordo com o comprimento calculado usando:Fórmula (4)Fórmula (5
A aproximação L ≈ ∑ k = 1 n Δ x k 2 + f x k - f x k - 1 2 do comprimento de arco não está dada como uma soma de Riemann.
Determine se a afirmação dada é verdadeira ou falsa. Explique sua resposta.O gráfico de y = 1 - x 2 é uma curva lisa em - 1,1 .
Encontre o comprimento de arco exato das curvas acima dos intervalos dados. 24 x y = y 4 + 48d ey = 2a t éy = 4 é