Enunciado
Cálculo - Cálculo Volume 1 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 4.8 - Ex. 23
23. Use o método de Newton para encontrar todas as raízes da equação com precisão de oito casas decimais. Comece fazendo um gráfico para encontrar a aproximação inicial
Passo 1
Fala aí, tudo bem com você?
Bom, essa questão é bem direta ao ponto!
Ela pede pra gente usar o método de Newton para encontrar, com precisão de oito casas decimais, a raiz de
E para isso, vamos relembrar o que é esse tal método de Newton.
Nele vamos considerar uma reta tangente à curva da função no ponto .
Depois devemos procurar a interseção de como o eixo , que será chamada de e verificar o quão próximo está da interseção da curva com o eixo .
Para encontrar , podemos fazer:
Depois, repetimos o processo, usando como uma segunda aproximação, fazendo:
E podemos repetir o processo quantas vezes for necessário. De modo geral, fazendo
E se ficar cada vez mais próxima da raiz de nossa curva à medida que cresce, fizemos que a sequência converge para .
Assim:
Perfeito. Então vamos usar essa ideia para encontrar o que o exercício pediu.
Passo 2
Nossa equação é a seguinte:
Antes de começar vamos esboçar um gráfico usando um programa computacional:
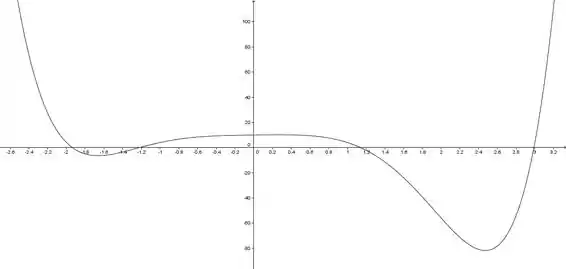
Considere a seguinte função:
Passo 3
Agora é só usar aquela formula da teoria:
Lá do Passo 1:
Derivando, usando a regra do expoente em cada termo, temos que
Arrumando as coisas, temos:
Olhando o gráfico, podemos ver que é interessante pegar os seguintes pontos:
;
Passo 4
Vamos começar com :
Fazendo as contas:
Para achar os próximos o processo é análogo. Logo,
Para :
Para :
Para :
Opa, como deu igual já podemos parar. Pois nos aproximamos o suficiente da raiz. Logo, a raiz aproximada de seis casas decimais será
Agora vamos fazer a mesma coisa para
Para :
Para :
Para :
Como , nossa raiz será .
Repetindo para :
Para :
Para :
Para :
Para :
Como , nossa raiz será
Por último, vamos fazer para o ponto :
Para :
Para :
Para :
Como , nossa raiz será
Resposta
As raízes aproximadas de seis casas decimais são , , e