Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 6.7 - Ex. 25

23-26 Encontre a massa e o centro de gravidade da lâmina dada de densidade δ .

25. A lâmina delimitada pelo gráfico de y = x e a reta y = 1 ; δ = 3 .

Passo 1

Vamos começar a desenhando o gráfico da região que delimita essa lâmina!

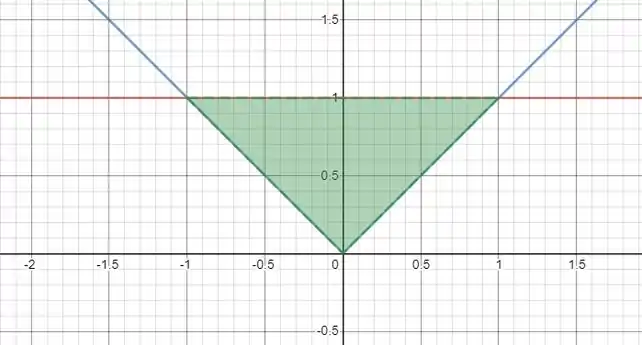
Essa função é simétrica em relação ao eixo y , então o x - = 0 e além disso, podemos fazer a área usando os intervalos de 0 a 1 e depois multiplicar por dois!

Passo 2

Agora vamos calcular a área dessa região R , vamos lá:

á r e a   d e   R = 2 ∫ 0 1 ( 1 - x ) d x = 2 x - x 2 2 1 0 = 2 1 - 1 2 - 2 0 - 0 2 2 = 2 × 1 2 = 1

Para calcularmos a massa, precisamos multiplicar a área pele densidade:

M a s s a   d e   R = 1 × 3 = 3

Passo 3

Vamos calcular agora o centroide, utilizando essas fórmulas:

x - = 1 á r e a   d e   R ∫ a b x f x - g ( x ) d x

y - = 1 á r e a   d e   R ∫ a b 1 2 f ( x ) 2 - g ( x ) 2 d x

O x - é zero, pois é simétrico em relação ao eixo y .

Temos que fazer o y ¯ , lembrando que vamos fazer de 0 a 1 e depois multiplicar por 2 .

y - = 2 × ∫ 0 1 1 2 1 - x 2 d x = 2 × 1 2 x - x 3 3 1 0 = 1 - 1 3 3 - 0 - 0 3 3 = 1 - 1 3 = 2 3

Botando em coordenadas, temos:

0 , 2 3

Resposta

3   ;   0 , 2 3

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Calcule a integral. ∫ 0 3 1 + 6 w 2 - 10 w 4 d w
Calcule a integral. ∫ 0 4 ( 3 t - 2 e t )d t
Calcule a integral. ∫ 0 π 5 e x + 3 s e nx d x
Calcule a integral. ∫ 1 2 1 x 2 - 4 x 3d x
Use a Parte 1 do Teorema Fundamental do Cálculo para encontrar a derivada da função.9) g ( s ) = ∫ 5 s t - t 2 8 . d t