Enunciado
Cálculo - Cálculo Volume 1 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 2.7 - Ex. 24
Uma estimativa anual da população da Bélgica, P (em milhares), de 1992 a 2000 é mostrada na tabela a seguir.
Encontre a taxa média do crescimento.
de 1992 a 1996 de 1994 a 1996 de 1996 a 1998.
Em cada caso, inclua as unidades.
Estime a taxa instantânea de crescimento de tomando a média de duas taxas médias de variação. Quais são as suas unidades?
Estime a taxa instantânea de crescimento em medindo a inclinação da tangente.
Passo 1
Olá, meu amigo. Vamos de mais uma resolução.
Aqui a gente tem de encontrar algumas informações relacionadas as taxas dos dados da tabela. Veja que taxa de variação é a divisão do dado que queremos analisar em relação a outro dado, a velocidade por exemplo é a taxa de variação do espaço pelo tempo.
Para resolvermos essa atividade, a taxa de variação aqui é a seguinte:
Em que é a variação de população em milhares de pessoas e é a variação do tempo em anos.
Passo 2
-
Fazendo a taxa, que é de 1992 a :
Substituindo os valores desses pontos:
Fazendo a taxa, que é de 1994 a
Substituindo os valores desses pontos:
Fazendo a taxa, que é de 1996 a
Substituindo os valores desses pontos:
Passo 3
- Faremos a média das duas últimas taxas que calculamos na letra , as taxas e pois são intervalos que contém o ano de e são taxas com intervalo de tempo com a menor distância entre eles.
- Para resolvermos essa letra iremos primeiro gerar o gráfico com os nossos dados, você poderá utilizar o seu software preferido para isso, o Excel é o mais aconselhado.
Passo 4
Vamos criar um triangulo utilizando a reta tangente ao ponto dado para criamos um triangulo retângulo e assim calcularmos a inclinação.
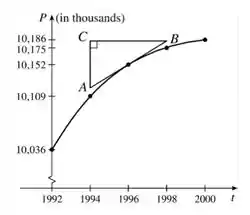
Estimando A como e B como , a inclinação em 1996 é a tangente do ângulo :
Resposta
taxa
taxa
taxa
Taxa instantânea pela média é igual a :
Taxa instantânea pela tangente é igual a :