Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 3.1 - Ex. 40
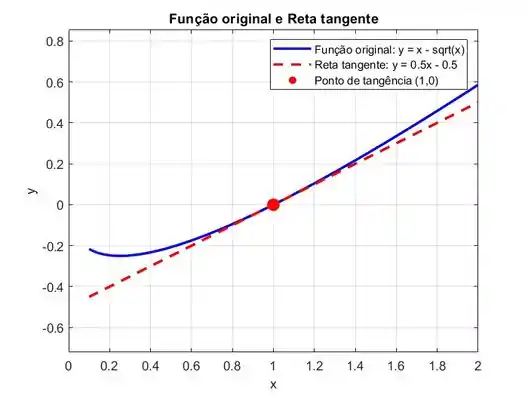
Encontre uma equação para a reta tangente à curva no ponto dado. Ilustre com o gráfico da curva e da reta tangente na mesma tela.
Passo 1
Oie galerinha, devemos achar a equação da reta tangente a uma curva.
Para termos a equação de uma reta, precisamos de um ponto e de sua inclinação.
O ponto já foi dado no enunciado.
Já inclinação pode ser obtida derivanda a função: ela é exatamente a derivada calculada no ponto.
A equação da reta com inclinação e que passa pelo ponto é:
Passo 2
Podemos reescrever a expressão da curva como
Vamos achar a inclinação derivando a função:
Substituindo ,
Passo 3
Usando , e na equação da reta:
Passo 4
O gráfico a seguir mostra a função original , a reta tangente , e destacar o ponto de tangência em .
Resposta
Exercícios de Livros Relacionados
Esboce o gráfico de uma função g que é continua no domínio ( - 5,5 ) e onde g 0 = 1 ,g ' 0 = 1 ,g ' - 2 = 0 , lim x → - 5 + g ( x ) = ∞ e lim x → 5 - g ( x ) = 3 .
Esboce o gráfico de uma função f que é continua no domínio - 2,2 e onde f ' ( 0 ) = - 2 , lim x → 2 - g x = ∞ ,f é contínua para todos os números no domínio, exceto ± 1 , e f é impar.
Gráfico da função f x = sin x - 1 10 0 0 sin ( 1000 x ) no retângulo de visualização [ - 2 π , 2 π ] ´pr [ - 4,4 ] . Qual a inclinação o gráfico parece ter na origem?
Seja l a reta tangente à parábola y = x 2 no ponto ( 1,1 ) . O ângulo de inclinação de l é o ângulo ϕ que l faz com a direção positiva do eixo x . Calcule ϕ com a precisão de um grau.
33-36 Encontre uma equação da reta tangente á curva no ponto dado. 33 .y = 2 x 3 - x 2 + 2 , ( 1 ,3 )