Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 3.1 - Ex. 39
Encontre uma equação para a reta tangente à curva no ponto dado. Ilustre com o gráfico da curva e da reta tangente na mesma tela.
Passo 1
Fala, galera! Beleza? Vamos resolver essa questão!
O enunciado pediu pra gente encontrar a reta tangente da curva no ponto e ilustrar essa curva junto com a reta.
Para termos a equação de uma reta, precisamos de um ponto e de sua inclinação. O ponto já foi dado no enunciado. Já inclinação pode ser obtida derivanda a função: ela é exatamente a derivada calculada no ponto.
A partir disso, temos que a equação da reta com inclinação e que passa pelo ponto é:
Então, vamos encontrar derivando e substituir tudo na função, junto com o ponto .
Vamos lá!
Passo 2
Vamos começar achando a inclinação da reta, derivando a função:
Agora para encontrar a inclinação no ponto dado, vamos substituir na derivada para obter:
Isso significa que nossa inclinação no ponto é
Tranquilo até aqui? ����
Passo 3
Usando , e na equação da reta, que vimos no passo , temos:
Aplicando a distributiva no produto:
E somando em ambos os lados, temos:
Bacana, não é? 😉
Passo 4
Esboçando a curva e a reta tangente .
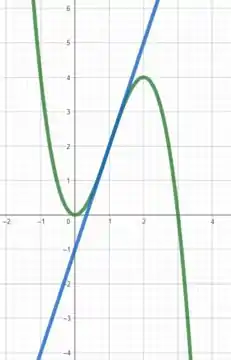
Prontinho, galera! Até a próxima! 😉