Enunciado
Cálculo - Cálculo Volume 1 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 3.6 - Ex. 36
Encontre as equações das retas tangentes à curva
Nos ponto e . Ilustre fazendo o gráfico da curva e de suas retas tangentes
Passo 1
Faala meus queridos!! Nessa questão queremos encontrar a equação da reta tangente à curva
Nos pontos e .
Para isso, vamos lembrar que a equação da reta tangente à uma curva num ponto é dada por:
Onde é a inclinação da reta tangente, que nada mais é que a derivada da função no ponto dado.
Ou seja, vamos precisar primeiro derivar essa função aí.
Passo 2
Primeiramente, devemos encontrar a derivada da função
Aqui vamos usar a regra do quociente que diz que:
Então, usando a regra do quociente
Passo 3
Agora, calcularemos os , para isso, basta substituirmos na expressão de e depois , então
E
Passo 4
Agora que já calculamos os valores de , podemos encontrar as equaçãoes das retas tangentes, primeiro calcularemos a equação da reta tangente ao ponto . Então
Passo 5
E agora para o ponto
Passo 6
Agora, mostraremos o esboço dos gráficos
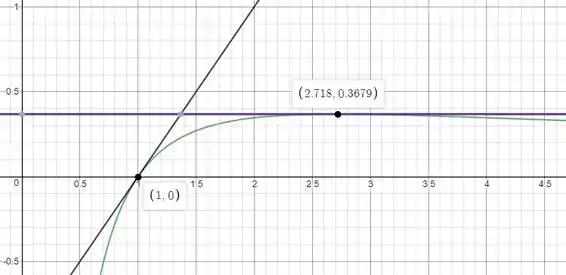
A reta quase horizontal em roxo é a reta tangente para o ponto .
A reta inclinada na diagonal em preto é a reta tangente para o ponto .E a a curva em verde é a curva .