Enunciado
Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 6.7 - Ex. 24
24. Resolva o Exercício 23 no caso em que a face do reservatório é um trapézio isósceles com 120 m de base maior no topo e 80 m de base menor e a distância entre as bases é de 40 m.
Passo 1
Vamos entender a figura do trapézio e depois calcular a força na face.
Passo 2
O esquema no trapézio é esse aqui ó:
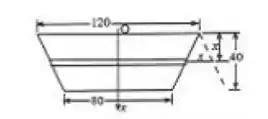
O reservatório está inclinado 30° na vertical e vai de 0 até 40. A profundidade é dada por:
Passo 3
Usando semelhança de triângulos, o comprimento é .
Então vamos calcular assim:
Passo 4
Resolvendo a integral...
Pronto
Resposta
Exercícios de Livros Relacionados
35- Placa retangular Em uma piscina com água a uma profundidade de 10 pés, calcule a força de fluido de um lado de uma placa retangular de 3 por 4 pés caso a placa repouse verticalmente no fundo da pi
36- Placa semicircular Calcule a força do fluido em um lado de uma placa semicircular com raio de 5 pés que repousa verticalmente sobre o seu diâmetro no fundo de uma piscina cheia de água até a profu
33- Placa triangular Calcule a forca de fluido em uma lado da placa do Exemplo 6 usando o sistema de coordenadas mostrado aqui.
38- Placa triangular girada A placa do Exercício 37 é girada 180° em torno da reta AB, de modo que parte dela fica de fora do lago, como n1ostrado a seguir. Que força a água exerce agora sobre um lado
39- Aquário da Nova Inglaterra O vidro de exibição típico de u1n tanque de peixes no Aquário da Nova Inglaterra em Boston tem 63 pol. de largura, e vai de 0,5 pol. até 33,5 pol. abaixo da superfície d