Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 5.4 - Ex. 46

Nos Exercícios de 45 a 52, uma função f e os números n , a e b são dados. Aproxime até quatro casas decimais a área da região limitada pela curva y = f ( x ) , o eixo x e as retas x = a e x = b fazendo o seguinte: divida o intervalo [ a , b ] em n subintervalos de Δ x unidades de igual comprimento e use uma calculadora para determinar a soma das áreas de n retângulos inscritos ou circunscritos (como indicado), cada um com Δ x unidades de largura.

46. f x = 1 x 2 ,   a = 1 ,   b = 2 ,   n = 1 2 , retângulos circunscritos.

Passo 1

Vamos seguir os passos do enunciado e dividir o intervalo em n = 1 2 subintervalos de Δ x unidades com:

Δ x = b - a n = 2 - 1 12 = 1 12

Como serão retângulos circunscritos e a função é decrescente em [ 1,2 ] , precisamos de f x i - 1 com:

x i - 1 = a + ( i - 1 ) Δ x = 1 + i - 1 12

f x i - 1 = 1 1 + i - 1 12 2 = 144 11 + i 2

Passo 2

Agora nós fazemos as somas das áreas dos retângulos.

A ≈ ∑ i = 1 12 f x i Δ x = 144 12 ∑ i = 1 12 1 11 + i 2 = 12 ∑ i = 1 12 1 11 + i 2

A ≈ 12 1 11 + 1 2 + 1 11 + 2 2 + 1 11 + 3 2 + 1 11 + 4 2 + 1 11 + 5 2 + 1 11 + 6 2 + 1 11 + 7 2 + 1 11 + 8 2 + 1 11 + 9 2 + 1 11 + 10 2 + 1 11 + 11 2 + 1 11 + 12 2

A ≈ 12 1 12 2 + 1 13 2 + 1 14 2 + 1 15 2 + 1 16 2 + 1 17 2 + 1 18 2 + 1 19 2 + 1 20 2 + 1 21 2 + 1 21 2 + 1 22 2 + 1 23 2 ≈ 0 , 5323

A ≈ 0,5323   u . a

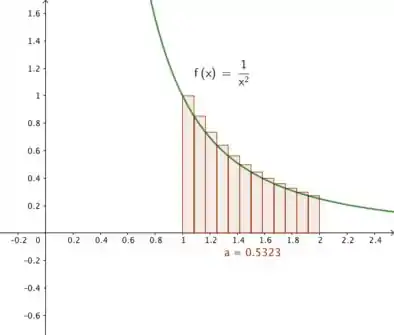
Resposta

A área é aproximadamente 0,5323   u . a .

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Use (a) a Regra do Trapézio, (b) a Regra do Ponto Médio e (c) a Regra de Simpson para aproximar a integral dada com o valor especificado de n . (Arredonde seu resultado para seis casas decimais.) ∫ 0
Use (a) a Regra do Trapézio, (b) a Regra do Ponto Médio e (c) a Regra de Simpson para aproximar a integral dada com o valor especificado de n . (Arredonde seu resultado para seis casas decimais.) ∫ 1
Calcule as aproximações T 8 e M 8 para a integral ∫ 0 1 cos ⁡ x 2 d x .Estime os erros nas aproximações na parte (a).Que tamanho de n devemos escolher para que as aproximações T n e M n para a integra
Use (a) a Regra do Trapézio, (b) a Regra do Ponto Médio e (c) a Regra de Simpson para aproximar a integral dada com o valor especificado de n . (Arredonde seu resultado para seis casas decimais.) ∫ 0
Use (a) a Regra do Trapézio, (b) a Regra do Ponto Médio e (c) a Regra de Simpson para aproximar a integral dada com o valor especificado de n . (Arredonde seu resultado para seis casas decimais.) ∫ 0