Enunciado
Cálculo - Boyce - Equações Diferenciais - Ed: 10º - Capítulo 9.8 - Ex. 12
12. (a) Seja . Encontre os pontos críticos e os autovalores correspondentes. O que você pode concluir dessa informação, se é que pode concluir alguma coisa?
(b) Desenhe a trajetória que começa na origem. Qual é o comportamento limite dessa trajetória? Para ver claramente o comportamento limite, você deve escolher uma janela com o intervalo de de modo a eliminar o comportamento transiente inicial.
(c) Escolha um ou dois outros pontos iniciais e desenhe as trajetórias correspondentes. O comportamento limite de cada uma é igual ao do item (b)?
(d) Note que existe um ciclo limite cuja bacia de atração é razoavelmente grande (mas não é todo o espaço ). Faça um gráfico de , ou em função de e estime o período de movimento em torno do ciclo limite.
Passo 1
A primeira coisa que devemos aqui é substituir as derivadas por , já que estamos buscando os valores dos pontos críticos:
Da segunda equação...
E da primeira equação, tiramos que...
Jogando esses dois últimos resultados na última equação...
Poxa! Uma equação do segundo grau:
Substituindo então o por e resolvendo a equação do segundo grau...
BELEZA! Substituindo então nas informações de e de ...
Os dois pontos críticos nesse caso então serão...
O jacobiano desse primeiro ponto será então...
Jogando no Wolfram para obter seus autovalores ganharemos...
MAS CALMA, meu Jovem! Temos um segundo ponto crítico e que certamente precisa ser avaliado também!
Calculando os seus autovalores por sua vez obteremos...
Passo 2
Conclusão:
Bem, obtivemos dois pontos críticos diferentes, onde para um deles...
Tivemos autovalores imaginários com a parte real negativa e a outra parte real positiva, é de se esperar que pontos próximos deste ponto referenciado aí em cima sejam assintoticamente estáveis, enquanto para regiões mais próximas do outro ponto seja instável.
Passo 3
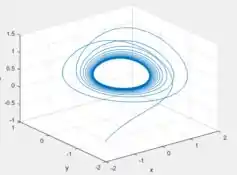
Utilizando o mesmo código do exercício anterior, só que substituindo o por na função de definição da derivada e, além disso, colocando o ponto inicial na origem e mandando o programa rodar, obteremos...
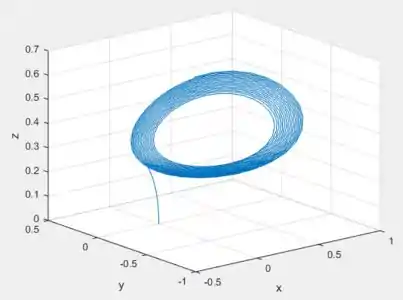
Veja que o comportamento limite dessa trajetória então é periódico.
Passo 4
Escolhendo o ponto ...
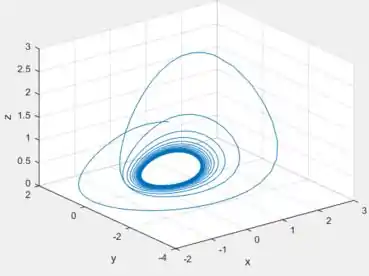
Agora escolhendo o ponto inicial ...
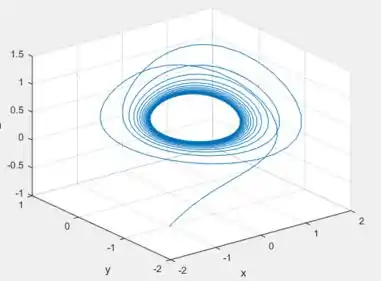
Em ambos percebemos que possuem comportamento bem similar, neh? De menos, é claro, nas partes iniciais, ou transitórias.
Passo 5
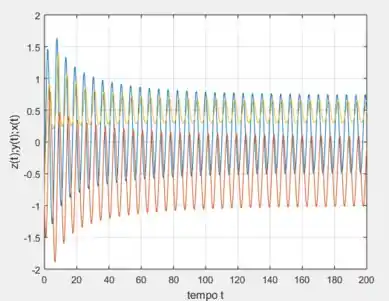
Com o ponto inicial mesmo, podemos desenhar os gráficos de , e em função de implementando o código na parte de plotagem de gráficos:
Quando você colocar o programa pra rodar, considerando de , vamos ter o seguinte gráfico com a implementação desse código:
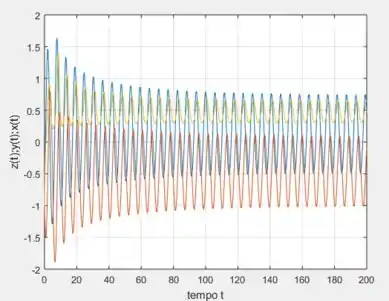
Ele está embolado assim, pois colocamos os três juntos em função do tempo. Em fim, dando um zoom apenas na parte Oscilatória após o transiente em ...
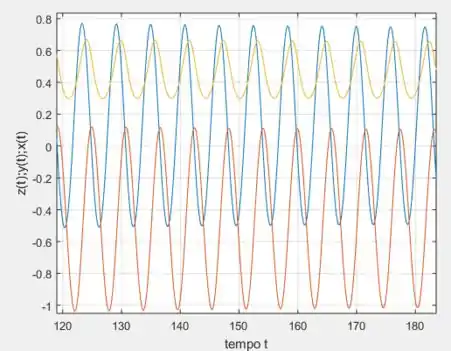
Veja que daí podemos estimar um período de aproximadamente , observando dois valores de mínimo para a curva laranja, por exemplo .
Resposta
Letra A:
Letra B:
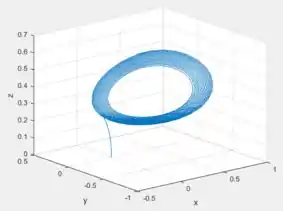
Letra C:
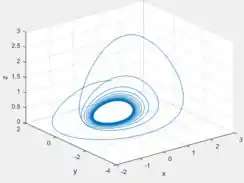
Letra D:
