Enunciado

Cálculo - Boyce - Equações Diferenciais - Ed: 10º - Capítulo 3.8 - Ex. 25

25. Suponha que o sistema do Problema 24 é modificado para incluir amortecimento e que o problema de valor inicial resultante é

(a) Gere, em um computador, o gráfico da solução do problema dado para diversos valores de entree e estime a amplitude da resposta estado estacionário em cada caso.

(b) Usando os dados encontrados em (a), faça o gráfico de em função de . Para que frequência a amplitude é máxima?

(c) Compare os resultados dos itens (a) e (b) com os resultados correspondentes para a mola linear.

Passo 1

Poxa vida, vamos trabalhar aqui com EDO não linear:

Por causa desse , saca?

INFELIZMENTE, resolver uma equação não linear de forma algébrica, como fazemos sem grandes mistérios com as EDO’s lineares, é muito difícil (isso se não impossível). Como o problema já nos dá uma autorização explicita de que podemos usar o computador, a coisa facilita, né?

Aqui, eu vou utilizar o WOLFRAMALPHA para resolver essa EDO, por dois motivos: é um site gratuito pra muitas aplicações matemáticas e também por que ele é simples de mexer. Mas lembrando de que você pode usar qualquer meio computacional ;)

Passo 2

Jogando WOLFRAMALPHA no Google e entrando na página, basta escrever a equação na barrinha de pesquisa delas do jeitinho que está aqui:

Usando as vírgulas para separar as condições! Perceba que já trocamos o por , que é o primeiro valor que o problema nos pediu. Ao dar Enter, o site vai te dar a resposta em gráfico:

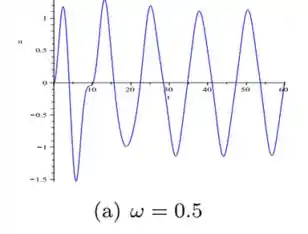
Trocando agora o por ...

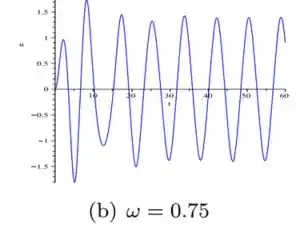
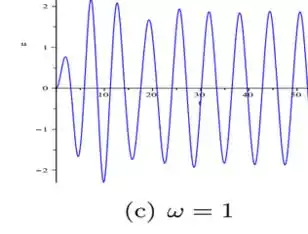
Por agora...

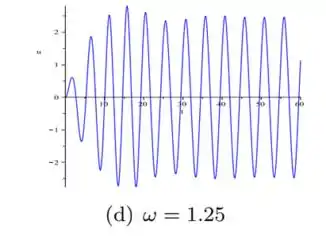
CALMA JOVEM! Eu sei, é bem chato ficar fazendo isso, mas está acabando, vamos lá: substituindo agora po ...

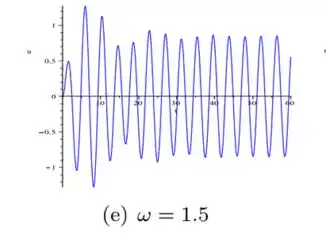
Por ...

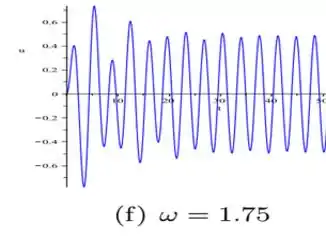
Finalmente por

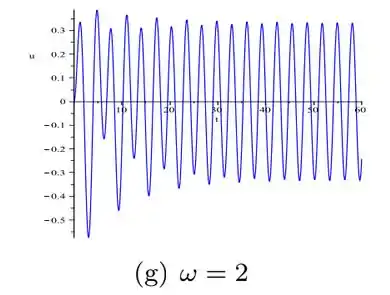
Beleza! O problema nos pede para variar de até então acabamos essa parte do problema.

Passo 3

Para retirar a informação de , basta a gente pagar a amplitude de cada figura. Mas atenção! Você tem que pegar esses valores da parte estacionária (Quando a função é uma senoidal bonitinha). Aqui montei uma tabelinha com os valores aproximados que eu encontrei:

Passo 4

Desenhando um gráfico aqui com esses dados da tabelinha...

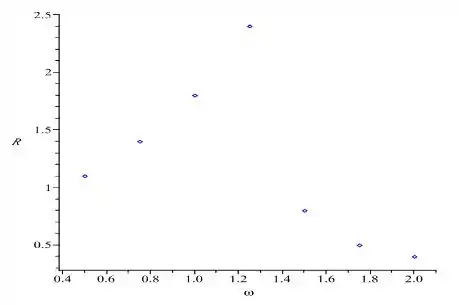
Bem, a frequência de ressonância é aquela que a amplitude é a maior possível. No nosso caso, o maior valor foi assumido em . Então podemos estimar que a frequência de ressonância é aproximadamente...

Passo 5

Comparando então esse nosso problema com um sistema linear massa mola, pela nossa teoria ganharíamos a seguinte curva...

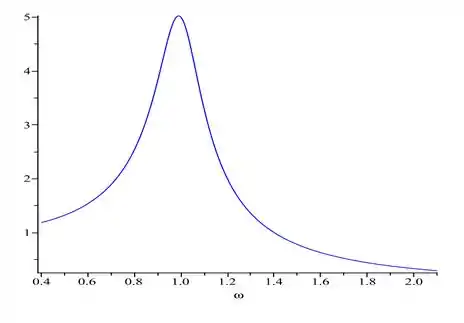
Vimos que essa curva no capítulo tem a seguinte equação de versus :

Resposta

Letra A:

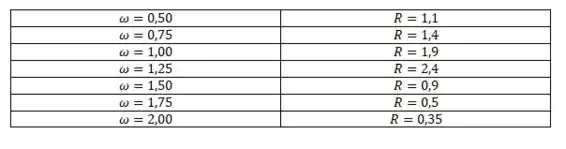
Letra B:

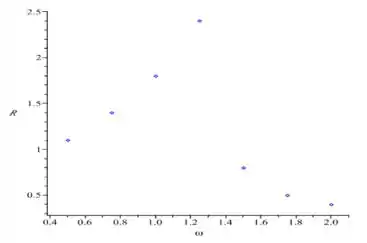
Letra C:

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Considere o problema de valor inicialSuponha que γ² Resolva o problema de valor inicial.

Considere o problema de valor inicialSuponha que γ² Escreva a solução na forma s(t) = R exp(–γt/2m) cos(μt – δ). Determine R em função de m, γ, k, s0 e υ0.

Considere o problema de valor inicialSuponha que γ² Investigue a dependência de R no coeficiente de amortecimento γ para valores fixos dos outros parâ-metros.

Um bloco cúbico de lado l e densidade de massa ρ por unidade de volume está flutuando em um fluido com densidade de massa ρ0 por unidade de volume, em que ρ0ρ. Se o bloco é mergulhado ligeiramente e d

Encontre a solução do Problema 5.