Enunciado
Cálculo - Boyce - Equações Diferenciais - Ed: 10º - Capítulo 7.6 - Ex. 28
28- Uma massa em uma mola com constante satisfaz a equação diferencial (veja a Seção )
Em que é o deslocamento da massa no instante a partir de sua posição de equilíbrio.
Sejam e ; mostre que o sistema resultante é
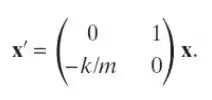
Encontre os autovalores da matriz para o sistema no item
Esboce diversas trajetórias do sistema. Escolha uma de suas trajetórias e esboce os gráficos correspondentes de e de em função de . Esboce ambos os gráficos no mesmo conjunto de eixos
Qual é a relação entre os autovalores da matriz de coeficientes e a frequência natural do sistema mola massa?
Passo 1
Como e então podemos dizer que:
E que:
(O enunciado está errado!)
Então, arrumando na matriz de coeficientes nós teremos:
Passo 2
Os autovalores dessa matriz serão:
Então os autovalores serão:
Passo 3
Vamos supor que e e ver o campo direcional:
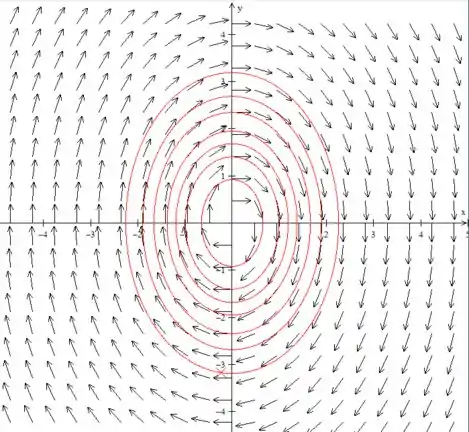
Quando teremos o seguinte caminho:
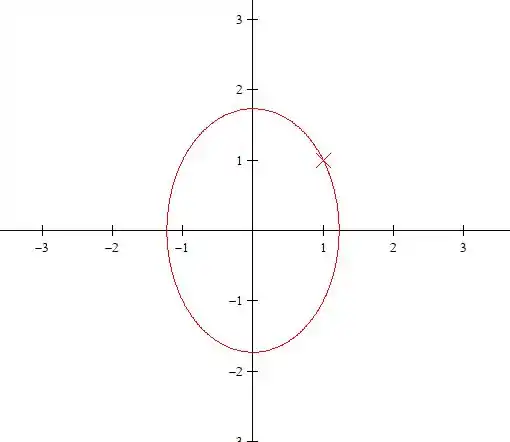
Com sendo a horizontal.
E a equação característica de e são iguais a:
Porém como é imaginário então os autovetores para serão iguais a:
Com autovetor sendo:
Então a solução será:
Arrumando:
Nos dando uma solução geral igual a:
Lembrando que sempre há outras formas de representar a mesma coisa!
E notou que a frequência natural é igual ao autovalor que é de ? É nessas horas que a matemática e a física se misturam, e isso diz muito sobre o conceito do autovalor.