Enunciado
Cálculo - Boyce - Equações Diferenciais - Ed: 10º - Capítulo 7.6 - Ex. 19
Em cada um dos problemas de 13 a 20, a matriz de coeficientes contém um parâmetro α. Em cada um desses problemas:
(a) Determine os autovalores em função de α.
(b) Encontre o valor ou valores críticos de α em que muda a natureza qualitativa do retrato de fase para o sistema.
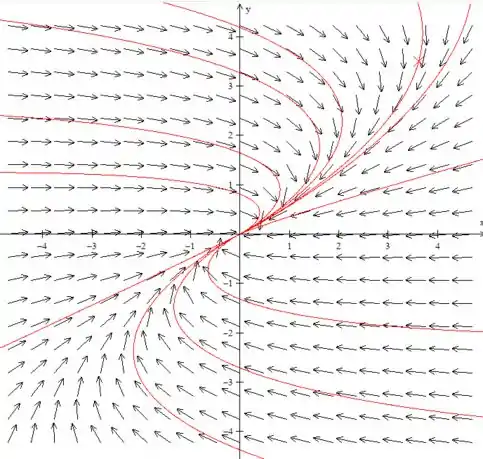
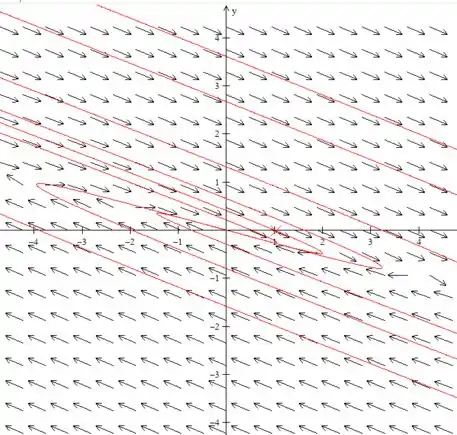
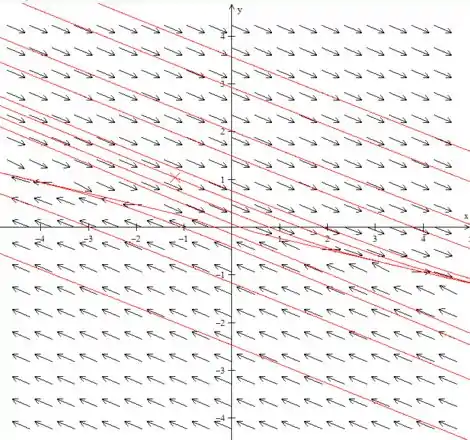
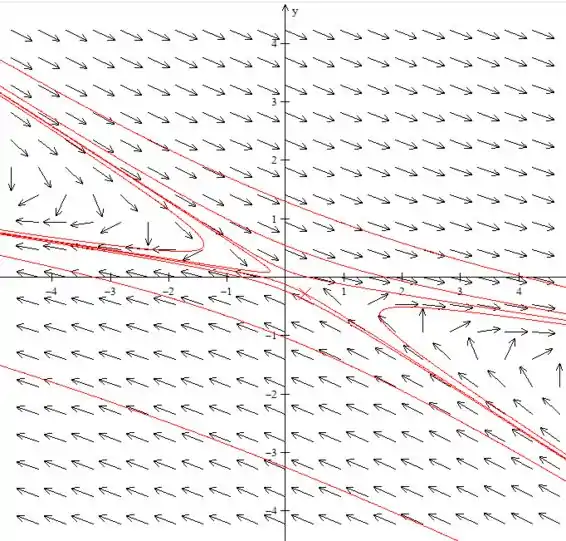
(c) Desenhe retratos de fase para um valor de α ligeiramente menor, e para outro valor ligeiramente maior, do que cada valor crítico.
Passo 1
Fazendo os autovalores dessa matriz aí nós teremos:
Que é só fazer essa determinante ai pai:
Agora fazendo Bhaskara teremos:
Passo 2
Esse sistema já é mais complexo, pois a equação do segundo grau dentro do delta tem raízes em :
Aproximadamente e .
De modo que temos um número negativo quando , logo o sistema terá polos complexos e conjugados. Fora desse intervalos temos um sistema com autovalores reais e distintos.
A instabilidade vem quando ultrapassamos a barreira de e começa a anular com , ou seja:
E que será e,
Além de que o termo nos dirá a estabilidade do sistema, então se o sistema será estável. De modo que tenhamos a seguinte tabela.
A diferença é que em
Temos apenas um autovalor positivo e em é certo que os dois autovalores são positivos
Passo 3
Para :
