Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 4.2 - Ex. 28

28. Suponha que um peso deva ser mantido 10m abaixo de uma reta horizontal A B por um fio com a forma de Y . Se os pontos A e B estão a uma distância de 8m um do outro, qual o fio de menor comprimento que pode ser usado?

Passo 1

Pra ficar mais fácil, vamos desenhar o problema e então fazer as contas pra achar o valor mínimo do fio.

Passo 2

Vamos considerar que o peso está no ponto P e que o segmento P D é perpendicular à reta A B . Como A B vale 8m e P D está no meio, temos A D = B D = 4 . O segmento C D chamamos de x e então, C P vale 10 - x . A quantidade total de fio será z :

z = A C + B C + P C

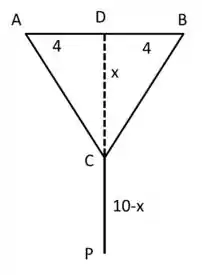
Passo 3

Agora, vamos escrever z como função de x para achar o valor mínimo de z .

Por Pitágoras, temos que A C = x 2 + 16 = B C e sabendo que P C = 10 - x :

z = 2 x 2 + 16 + 10 - x

Pra achar o valor mínimo, derivamos isso e igualamos a zero, certo?

z ' = 2 x x 2 + 16 - 1 = 0

2 x x 2 + 16 - 1 = 0

2 x x 2 + 16 = 1

2 x = x 2 + 16

4 x 2 = x 2 + 16

x 2 = 16 3

x = 4 3 3

Passo 4

Agora, avaliamos z   (comprimento total de fio) nos pontos que ele pode assumir ( z = 0 ) e ( z = 10 ) , e também no ponto x que achamos pra ver se realmente ele minimiza z . Ok?

z 0 = 2 4 + 10 = 18

z 10 = 2 116 = 21,5

z 4 3 3 = 2 64 3 + 10 - 4 3 3 = 10 + 4 3 = 16,9

Então o x que encontramos nos dá o menor comprimento total de fio, ou seja o menor valor de z , que é 16,9m.

Resposta

O fio de menor comprimento de ter 10 + 4 3 = 16,9 m .

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Ache as dimensões do cone circular reto com menor volume que possa circunscrever um cilindro circular reto com r cm de raio e h cm de altura.
Um pedaço de fio de 20 cm deve ser cortado em dois e cada parte é dobrada, tomando a forma de um quadrado. Como deve ser cortado o fio de modo que a área total dos quadrados seja a menor possível?
Se x 3 + y 3 - 3 x y 2 + 1 = 0 , ache d y no ponto 1 ,1 se d x = 0,1 .
Um recipiente na forma de um cubo com um volume de 1.000 c m 3 deve ser fabricado com seis quadrados iguais de um material que custa 20 centavos por centímetro quadrado. Com que precisão deve ser calc
(a) Se f x = 3 x + 4 | x - 1 | , prove que f tem um valor mínimo absoluto de 3. (b) Se g x = 4 x + 3 | x - 1 | , prove que g tem um valor mínimo absoluto de 3. (c) Se a0 e b0, e se h x = a x + b | x -