Enunciado
Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 4.Revisão - Ex. 87
(a) Se , prove que tem um valor mínimo absoluto de 3. (b) Se , prove que tem um valor mínimo absoluto de 3. (c) Se a > 0 e b > 0, e se , prove que tem um valor mínimo absoluto que é menor dos dois números a e b.
Passo 1
Para resolver o item (a) basta encontrar os pontos críticos da equação dada. Porém, lembre-se que não podemos usar derivada para achar esses pontos pois a função é modular.
Sabendo disso os pontos críticos são os pontos na qual um dos termos dão zero, assim, quando x=1 ou quando x=0, haverá descontinuidade no gráfico, como pode ser visualizado na imagem abaixo:
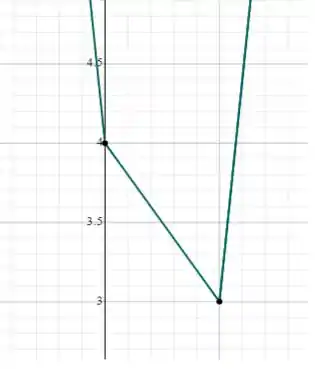
Dessa maneira, bastar substituirmos o valor dos pontos críticos na função e verificar qual é o menor deles. Logo,
Passo 2
Da mesma maneira é feita o item (b). Assim os pontos críticos da função são, x=1 e x=0.
Com isso, basta substituirmos os pontos críticos na função, assim:
Logo, o valor mínimo da função é 3.
Passo 3
A resolução do item (c) não difere do itens anteriores, sabendo disso, vamos achar os pontos críticos da função , que são os mesmo do itens anteriores, x=0 e x=1.
Substituindo os valores na função, temos:
Note que, o valor mínimo absoluto é o menor dos dois número a e b, o que prova a questão.
Resposta
Ei, a resposta está no passo a passo :)