Enunciado
Cálculo - Cálculo Volume 1 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 3.4 - Ex. 28
28.(a) Se , encontre .
(b) Verifique que sua resposta para a parte (a) é razoável fazendo os gráficos de e para
Passo 1
Olá, meu querido amigo. Iremos, eu e você, resolvermos essa atividade.
Aqui a gente tem que calcular a derivada da função:
Por termos um produto entre funções, precisaremos utilizar da regra do produto para derivarmos corretamente.
É assim, dada e , a derivada do produto entre essas funções é:
Para construirmos o gráfico iremos utilizar o GeoGebra, um software matemático, fácil, gratuito e online.
Passo 2
(a)Fazendo aquela anotação esperta de e :
Aplicando a regra de derivadas para polinômios:
A derivada de funções trigonométricas é tabelada:
Substituindo na expressão do produto de derivada!
A primeira parte está feita, vamos para a análise do gráfico!
Passo 3
(b)
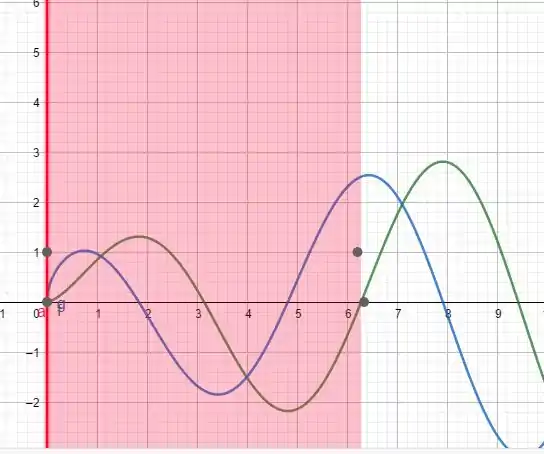
Tudo conforme imaginamos, quando a função tem valor máximo ou valor mínimo, é igual a zero.
Em vermelho é o intervalo de a
Resposta
(a)
(b)
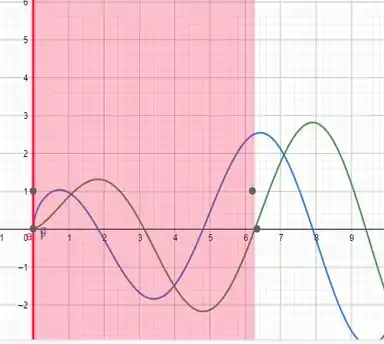
Tudo conforme imaginamos, quando a função tem valor máximo ou valor mínimo, é igual a zero.
Em vermelho é o intervalo de a