Enunciado
Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 5.5 - Ex. 30
29-32 Determine se a afirmação falsa é verdadeira ou falsa. Explique a resposta.
30- Vale
Passo 1
Essa questão é puramente conceitual, então vamos com calma para não nos embolarmos.
O Teorema 5-5-6 a)
Diz que: Se for integrável em e em cada de , então:
Passo 2
Caso você não tenha entendido muito bem o teorema ele diz que, se uma função for positiva nos intervalos de integração, então a integral dessa função também será positiva!
Para provarmos então que a integral abaixo:
É positiva, temos que provar que a função abaixo:
Também é positiva no intervalo
Passo 3
Temos que demonstrar que a função
É positiva em .
Ora, a função do denominador é sempre positiva, pois é uma raiz!!
Então só precisamos provar que é positivo em !!
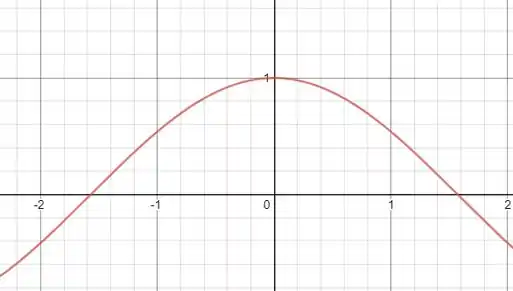
O gráfico de nos mostra algo bem legal! Repara lá!
Entre é positivo, portanto a função é positiva para qualquer valor entre
Se a a função é positiva para qualquer valor entre , então podemos afirmar que
Portanto essa afirmação é verdadeira!!
Resposta
Verdadeira