Enunciado
Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 5.5 - Ex. 32
29-32 Determine se a afirmação falsa é verdadeira ou falsa. Explique a resposta.
32- A função
É integrável em qualquer intervalo
Passo 1
Essa questão é puramente conceitual, então vamos com calma para não nos embolarmos.
Desenharemos o gráfico dessa função e usaremos o fato de que uma função integrável se tiver um número finito de descontinuidade em , mas for limitada em .
Passo 2
Vou desenhar inicialmente o gráfico, que é simples de fazer, para , temos um parte de uma parábola e para , temos uma função constante e nula.
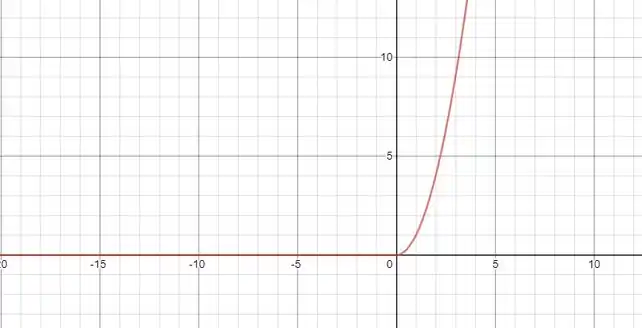
A nossa função está em vermelho, e o único ponto em que poderíamos ter uma descontinuidade é o ponto , porém essa função não é descontínua nesse ponto.
Então, podemos afirmar que a função possui um número finito de descontinuidade, que são zero pontos de descontinuidade, então número de descontinuidade igual a .
Passo 3
As funções continuas são sempre limitadas num intervalo fechado .
Essa função é contínua, pois não possui pontos de descontinuidade, então podemos afirmar que para qualquer intervalo fechado a função será limitada.
Essa função possui número finitos de descontinuidade e ainda é limitada, então com toda certeza ela é integrável.
Com tudo que falamos, e não foi pouco hein, podemos concluir que essa afirmação é verdadeira.
Resposta
Verdadeira