Enunciado
Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 6.7 - Ex. 33
31-34 Verdadeiro/Falso Determine se a afirmação dada é verdadeira ou falsa. Explique sua resposta [No exercício 34, suponha que o quadrado girado fique no plano direitado eixo
33. O centroide de um triângulo equilátero é a interseção das medianas do triângulo
Passo 1
Vamos começar a desenhando o gráfico esse triângulo.
Passo 2
Precisamos traçar a primeira mediana e ver se ela divide esse triângulo em duas partes simétricas, vamos fazer a mediana .
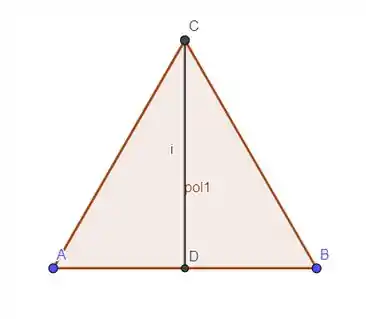
O triângulo ACD é igual ao triângulo CBD, pois
,pois o triângulo é equilátero
, pois o segmento é uma mediana.
O triângulo é simétrico em relação a mediana ! a mediana é uma reta de equilíbrio, mas o que isso quer dizer?
Quer dizer que o centroide está no segmento .
Vamos agora traçar a mediana e verificar se esse segmento divide o triângulo em dois iguais!
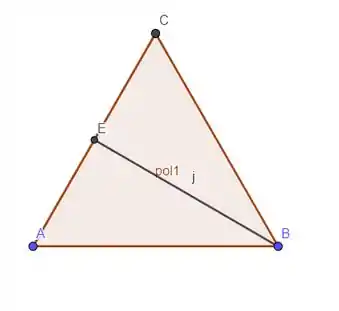
Esses dois triângulos formados são iguais
, já que esse triângulo é equilátero.
, já que o segmento é a mediana!
Como esses dois triângulos são simétricos, podemos afirmar que o centroide está na reta .
Passo 3
Agora para finalizar, vamos fazer a mediana !
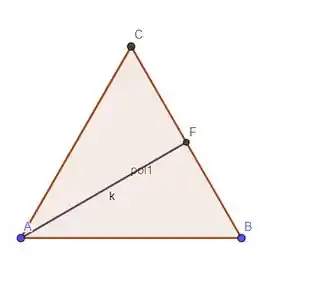
Esses dois triângulos formados são iguais
, já que esse triângulo é equilátero.
, já que o segmento é a mediana!
Como esses dois triângulos são simétricos, podemos afirmar que o centroide está na reta .
O centroide tem de estar na mediana , e , então o centroide está na interseção de todas essas medianas.