Enunciado
Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 4.3 - Ex. 41
39-44. Obtenha um gráfico da função e identifique a localização de todos os pontos de extremos relativos e de inflexão. Confira seu trabalho com um recurso gráfico.
41.
Passo 1
Então pessoal, esse tipo de questão é bastante característico do conteúdo de máximos e mínimos, então vamos resolver a questão passo a passo e com cuidado para arrasarmos nas próximas questões com facilidade, ok? Show, bora lá!
A função que nos foi dada é a seguinte:
Caso não se lembre, para identificarmos os pontos de extremos relativos de uma função devemos fazer uma análise dos pontos críticos da mesma, isto é, analisar os pontos em que ou os pontos em que não existe! Ademais, para identificarmos os pontos de inflexão devemos fazer a mesma análise dos extremos, mas agora para , ok? Vamo que vamo!
Passo 2
Derivando a nossa função, teremos:
Se igualarmos isso a zero, obteremos a seguinte relação:
Ou seja:
Como a questão não especifica um intervalo, vamos adotar os valores de para voltas, beleza? De acordo com o que estudamos em trigonometria, quais são os ângulos que satisfazem essa igualdade? São esses aqui, ó:
Então esses são os pontos de extremo relativo da nossa função, galera!
Passo 3
Os pontos de inflexão de uma função são os pontos no qual a função muda de concavidade, ou seja, sai de e vira e vice-versa! Derivando a nossa derivada, teremos:
Se igualarmos a zero, obteremos a seguinte relação:
Ou seja:
Como a questão não especifica um intervalo, vamos adotar os valores de para voltas, beleza? De acordo com o que estudamos em trigonometria, quais são os ângulos que satisfazem essa igualdade? São esses aqui, ó:
E esses são nossos pontos de inflexão, pessoal! 😉
Esboçando o gráfico da função para conferirmos nosso trabalho, teremos algo assim:
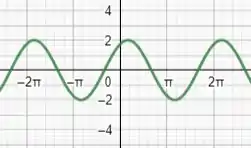
E está aí nossa resolução, guys!
Resposta
Pontos de extremos relativos: ;
Pontos de inflexão: ;
Gráfico da função:
