Enunciado
Cálculo - Um curso de Cálculo Volume 1 - 5ª Edição - Hamilton Luiz Guidorizzi- Ed: 5º - Capítulo 11.6 - Ex. 26
Uma partícula desloca-se sobre o eixo com velocidade , . Calcule o espaço percorrido entre os instantes e .
Passo 1
O espaço percorrido pela partícula é:
Olhando o gráfico de velocidade:
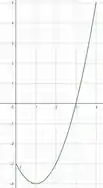
É possível observar que a velocidade é negativa no intervalo e positiva no intervalo .
Passo 2
Assim, o espaço percorrido fica:
Resposta
Exercícios de Livros Relacionados
Uma janela de observação em um submarino é um quadrado com 2p é s é de lado. Usando ρ 0 como o peso específico da água do mar, encontre a força exercida pelo fluido sobre a janelaquando o submarino es
(a) Mostre: Se o submarino do Exercício 20 estiver descendo verticalmente a uma taxa constante, então a força do fluido sobre a janela aumenta a uma taxa constante.(b) Com que taxa a força do fluido s
Por quantos pés devemos baixar a água da piscina do Exercício 17 para que a força no fundo seja reduzida por um fator de 1 2 ?
A figura abaixo mostra uma piscina retangular cujo fundo é um plano inclinado. Encontre a força da água sobre o fundo quando a piscina estiver cheia até o topo.
Use os valores dados de aeb para expressar os limites seguintes como integrais. (não calcule as integrais) lim max Δ x k → 0 ∑ k = 1 n s e n 2 x k * Δ x k ;a = 0 ,b = π 2