Enunciado
Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 6.1 - Ex. 32
32. Ache o volume do sólido gerado pela rotação, em torno do eixo y , da região limitada pela reta que passa por (1,3) e (3, 7) e pelas retas y = 3 , y = 7 e x = 0.
Passo 1
Para conseguirmos resolver o que o enunciado nos pede, seria ideal desenhar a região da qual ele está falando para conseguirmos visualizar melhor o problema. Neste tipo de questão de volume de sólido obtido a partir da rotação sobre algum eixo devemos levar em consideração sobre qual eixo está sendo rotacionado. Como neste caso está sendo em torno do eixo y, devemos encontrar uma função que descreve a variação do raio da região em questão na medida em que eu vou variando o meu valor de y.
Devemos ter em mente também que o volume de um sólido obtido pela rotação em torno de um eixo qualquer é dado por .
Passo 2
Um esboço da região em que o enunciado se trata pode ser representado pela seguinte forma:
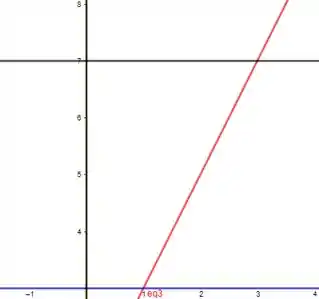
Passo 3
A próxima etapa para resolução é determinar qual é a função que descreve a variação do raio do sólido em questão. Esta função pode ser obtida a partir da determinação da equação da reta que passa pelos pontos dado no enunciado da seguinte forma:
A partir da resolução do determinante acima obtem-se que :
Ou seja, obtemos a nossa função que descreve como x muda na medida em que y varia.
Passo 4
Assim, o volume da região em questão é obtido da seguinte forma :
Logo, o volume do sólido de revolução obtido é .