Enunciado
Cálculo - Cálculo Volume 2 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 15.4 - Ex. 33
33- Uma piscina circular tem de diâmetro. Sua profundidade é constante na direção leste-oeste e aumenta linearmente de no término sul para no término norte. Determine o volume da água da piscina.
Passo 1
Olá, tudo tranquilo? Vamos ver o que a questão quer
Basicamente, ela diz que tem uma piscina com o formato de um círculo, com diâmetro de , profundidade constante no sentido leste-oeste e vai aumentando de forma constante de na borda sul até na borda norte.
E com base nisso, devemos achar o volume da piscina.
Bem, o volume utilizando integral dupla é assim:
Sendo a altura do sólido, que nesse caso é a profundidade da piscina.
Como estamos falando de círculo, usaremos as coordenadas polares para facilitar as contas.
Portanto, o caminho a seguir será esse:
Faremos um esboço da região que o enunciado falou, pois facilita muito visualizar o problema, depois acharemos nossa função de profundidade, depois montaremos a integral e resolveremos ela.
Show?
Passo 2
Vamos então, esboçar essa região!
O principal erro dessa questão é achar que a piscina descrita no enunciado é puramente um cilindro o que não é verdade a melhor forma de representar essa piscina é com o que seguinte corte no cilindro abaixo.
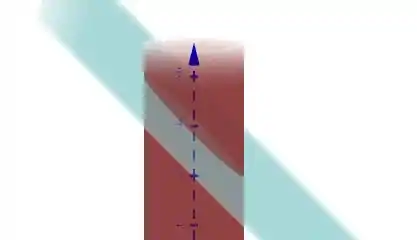
Pois assim, caso estivéssemos dentro da piscina e andássemos de leste a oeste, a profundidade mudaria. Mas se andássemos de norte a sul, a profundidade seria a mesma!
Imagine que estaremos passando um plano linear e estaremos interessados somente na parte de cima do cilindro.
Passo 3
Agora, vamos achar a função da nossa profundidade. Na figura planificada da piscina, o círculo tem raio de e está centrado no eixo
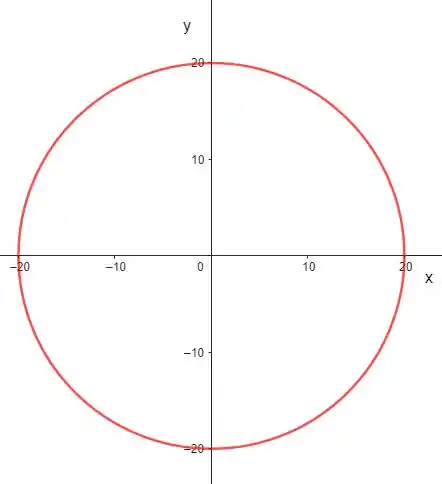
Se considerarmos como leste e oeste, e como eixo norte e sul. E a profundidade como positivo (sentido oposto ao desenhado).
Teremos que a piscina terá profundidade de em e profundidade de quando . Todos em
Matematicamente nossa função de profundidade terá:
Como a profundidade varia constantemente, teremos uma função desse tipo
Que é a equação de uma reta e aparece , pois como é o eixo norte e sul, ele não interfere na profundidade.
Para achar o coeficiente angular é fácil, só precisamos dividir a diferença de entre dois pontos e dividir pela diferença de entre dois pontos.
Temos então
Para achar o coeficiente linear, precisamos substituir algum ponto que achamos na equação, faremos para , assim
Isolando
Temos então,
Pronto, achamos nossa função da profundidade!
Passo 4
Agora, vamos montar nossa integral!
Já sabemos que , que é , assim
Como estamos em uma região circular, vamos usar coordenadas polares, temos então que
Portanto,
Onde a região é o círculo de raio igual a , e como temos um círculo completo, o intervalo de e iguais a:
Logo a integral dupla fica:
Ou seja:
Passo 5
Resolvendo a integral
Primeiro em relação à :
Aplicando os limites:
Resolvendo em relação à :
Aplicando os limites
Prontinho!