Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 2 - 6ª Edição - James Stewart- Ed: 6º - Capítulo 15.4 - Ex. 16

Utilize a integral dupla para determinar a área da região.

A região delimitada pela curva r = 4 + 3 cos ⁡ θ .

Passo 1

A questão pede para calcular a área da região delimitada pela cardioide r = 4 + 3 cos ⁡ θ dada em coordenadas polares. Fazendo θ variar de 0 até 2 π , temos que

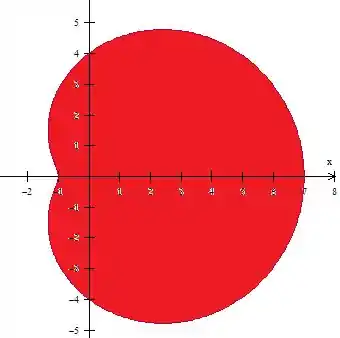
Assim, como em coordenadas polares d A = r   d r   d θ :

A = ∫ 0 2 π ∫ 0 4 + 3 cos ⁡ θ r   d r   d θ

Passo 2

Calculando primeiro a integral em r :

A = 1 2 ∫ 0 2 π 4 + 3 cos ⁡ θ 2   d θ

Note que

4 + 3 cos ⁡ θ 2 = 16 + 24 cos ⁡ θ + 9 cos 2 ⁡ θ = 16 + 24 cos ⁡ θ + 9 2 1 + cos ⁡ 2 θ

Assim,

A = 1 2 ∫ 0 2 π 41 2 + 24 cos ⁡ θ + 9 2 cos ⁡ 2 θ d θ = 41 4 ⋅ 2 π = 41 π 2

Resposta

41 π 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Calcule a integral dada, colocando-a em coordenadas polares. ∬ De - x 2 - y 2d A , onde D é a região delimitada pelo semicírculo x = 4 - y 2 e o eixo y .
Use uma integral dupla para encontrar a área da região:A região dentro do círculo x - 1 2 + y 2 = 1 e fora do círculo x 2 + y 2 = 1 .
Utilize a integral dupla para determinar a área da região.A região dentro do círculo r = 1 + cos ⁡ θ e fora do círculo r = 3 cos ⁡ θ .
Calcule o valor da integral múltipla. ∫ ∫ D xd A Onde D é a região do primeiro quadrante que se encontra entre os círculos x 2 + y 2 = 1 e x 2 + y 2 = 2 .
Descreva a região cuja área é dada pela integral int_0^((pi)/(2)) int_0^(s e n (2 theta)) r d r d theta