Exercícios de Mudança para Coordenadas Polares - Lista de Exercícios Resolvida
Questão 1
Calcule
Onde é a região no primeiro quadrante limitada pelo semi-círculo .
Ver solução completaQuestão 2
Calcule , onde é a região do primeiro quadrante situada entre as circunferências e .
Ver solução completaQuestão 7
7 - Usando coordenadas polares, calcule:
e) , onde é a região limitada por .
Ver solução completaQuestão 8
Considere a região plana dada por:
E a integral dupla
- Esboce a região
- Expresse a integral como uma integral iterada nas variáveis cartesianas e y, integrando primeiro com respeito a e em seguida com respeito a (Obs.: Neste item não é pedido o cálculo da integral).
- Expresse a integral como uma integral iterada nas variáveis polares e . (Obs.: Neste item não é pedido o cálculo da integral)
- Calcule (usando o método que preferir)
Questão 10
Calcule
Onde é a região no primeiro quadrante limitada pelo semi-círculo .
Ver solução completaQuestão 11
Utilize coordenadas polares para combinar a soma
Em uma única integral. Em seguida, calcule essa integral.
Ver solução completaQuestão 13
Por meio de coordenadas polares, calcule a integral
Em que R é a região limitada pelo triângulo de vértices .
Ver solução completaQuestão 18
Calcule a área da figura plana limitada pela curva dada pela equação .
Ver solução completaQuestão 21
Calcule a integral iterada, convertendo-a antes para coordenadas polares.
a)
Ver solução completaQuestão 22
Calcule a integral iterada, convertendo-a antes para coordenadas polares.
b)
Ver solução completaQuestão 23
Envolvendo coordenadas polares, calcule:
a) , onde é a região do primeiro quadrante situada entre as circunferências e .
Ver solução completaQuestão 26
Questão 4: Calcule a integral dada, colocando-a em coordenadas polares:
Onde é a região acima do eixo e dentro da circunferência .
Ver solução completaQuestão 27
Sejam . Transformar em coordenadas cartesianas e descrever a seguinte curva, dada em coordenadas polares por
Ver solução completaQuestão 29
7 - Usando coordenadas polares, calcule:
g) , onde é a região limitada por . Interprete o resultado geometricamente.
Ver solução completaQuestão 31
- Uma placa tem a forma da região limitada pelas retas , , e .
A densidade em cada ponto é inversamente proporcional a distância à distância do ponto à origem. Determine a massa da placa.
Ver solução completaQuestão 32
Use coordenadas polares para calcular a área da região interior ao círculo , exterior ao círculo
Ver solução completaQuestão 33
- Inverta a ordem de integração (Tipo I para tipo II) e calcule:
- Usando coordenadas polares calcule:
Ver solução completaQuestão 35
Calcule onde é a região do plano no interior da cardióide e no exterior do círculo . Sugestão: use coordenadas polares
a)
b)
c)
d)
e)
Ver solução completaQuestão 36
Calcule onde é a região de interna ao cilindro , externa ao cilindro , limitada acima pelo semicone e abaixo pelo paraboloide .
a)
b)
c)
d)
e)
Ver solução completaQuestão 38
5 – Calcular:
Em que é a região do primeiro quadrante delimitada por , , e .
Ver solução completaQuestão 39
Questão 2. Use técnicas de integração para determinar a área da região plana delimitada pelos círculos e e que está entre as retas e .
Ver solução completaQuestão 40
(4) Seja a região contida no primeiro quadrante do plano, limitada pela curva , pela reta e pela reta . Marque a opção que representa a integral após mudar para coordenadas polares.
Questão 41
Questão 3:
Considere a região plana onde:
e
- Esboce e determine a fronteira de através de igualdades e desigualdades.
- Calcule
Questão 42
Questão 1: Calcule a integral dupla da função no disco unitário centrado na origem.
Ver solução completaQuestão 43
Questão 3: Calcule
Onde é a região do primeiro quadrante entre as circunferências e .
Ver solução completaQuestão 44
6) Arraste e solte, nos campos correspondentes, o valor correto de cada elemento, conforme as opções disponíveis.
b) onde:
e ;
Ver solução completaQuestão 45
Calcule a área da região situada fora do círculo de equação e dentro do círculo de equação
Ver solução completaQuestão 46
Considere a região do plano limitado pela curva
- Esboce em coordenadas cartesianas e polares.
- Calcule
Questão 47
Transforme para o sistema de coordenadas polares a integral
Em seguida, calcule o seu valor.
Questão 48
Calcule a integral
Onde é a região no primeiro quadrante limitada pelas retas , , e pelos círculos e .
Ver solução completaQuestão 49
Considere e a integral dada por
- Usando coordenadas polares calcule . Justifique.
Questão 50
- Calcule a integral abaixo
Ondeé a região contida no primeiro quadrante do plano cartersiano que está dentro do círculo de centro e raio e fora do círculo de mesmo centro e raio .
Ver solução completaQuestão 52
7 - Usando coordenadas polares, calcule:
c) , onde é a região limitada por e .
Ver solução completaQuestão 54
8 - Uma região é mostrada em cada um dos gráficos da figura abaixo. Decida se você deve usar coordenadas polares ou retangulares e escreva os limites de integração da integral iterada , onde f é uma função arbitrária qualquer contínua em R.
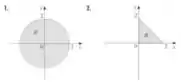
Questão 55
7 - Usando coordenadas polares, calcule:
d) , onde é a região limitada por
Ver solução completaQuestão 56
7 - Usando coordenadas polares, calcule:
f) , onde é a região limitada por .
Ver solução completaQuestão 57
Calcule onde é a região do plano no interior da cardióide e no exterior do círculo . Sugestão: use coordenadas polares
a)
b)
c)
d)
e)
Ver solução completaQuestão 59
Calcule a integral, colocando-a em coordenada polar:
Onde é a região anular .
Ver solução completaQuestão 62
(Capítulo 15.4 – Exercício 32) Calcule a integral iterada, convertendo-a antes para coordenadas polares.
Ver solução completaQuestão 63
(Cap 15.4 – Ex 2) Uma região é mostrada na figura. Decida se você deve usar coordenadas polares ou retangulares e escreva como uma integral iterada, onde é uma função qualquer contínua em .
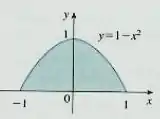
Questão 64
(Cap 15.4 – Ex 4) Uma região é mostrada na figura. Decida se você deve usar coordenadas polares ou retangulares e escreva como uma integral iterada, onde é uma função qualquer contínua em .
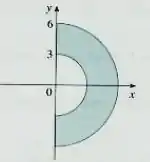
Questão 65
(Capítulo 15.4 – Exercício 29) Calcule a integral iterada, convertendo-a antes para coordenadas polares.
Ver solução completaQuestão 66
(Cap 15.4 – Ex 9) Calcule a integral dada, colocando-a em coordenadas polares.
Onde R é a região do primeiro quadrante entre os círculos com centro a origem e raios 1 e 3.
Ver solução completaQuestão 67
(Capítulo 15.4 – Exercício 40)
(a) Definimos a integral imprópria (sobre todo o plano )
onde é o disco com raio e centro na origem. Mostre que
(b) Uma definição equivalente da integral imprópria da parte (a) é
onde é o quadrado com vértices . Use esse resultado para mostrar que
(c) Deduza que
(d) Fazendo a mudança de variável , mostre que
(Esse é um resultado fundamental em probabilidade e estatística.)
Ver solução completaQuestão 68
(Cap 15.4 – Ex 7) onde é a metade superior do disco com centro na origem e raio 5.
Ver solução completaQuestão 69
(Cap 15.4 – Ex 8) Calcule a integral dada, colocando-a em coordenadas polares.
Onde R é a região do primeiro quadrante limitada pelo círculo e as retas e .
Ver solução completaQuestão 71
Calcule , em que é a região do primeiro quadrante limitada pelo círculo . Esboce a região .
Ver solução completaQuestão 73
Uma placa plana tem a forma da região que ocupa o primeiro quadrante entre as circunferências e . Se a densidade em cada ponto da placa é igual à soma das coordenadas do ponto, determine a massa da placa.
Ver solução completaQuestão 78
Mude a integral cartesiana para uma integral polar equivalente e calcule a integral polar de:
Questão 79
Calcule a massa de uma lâmina delimitada por , se a densidade em um ponto é proporcional à distância desse ponto a .
Ver solução completaQuestão 80
Considere a região plana
E a integral dupla
- Esboce a região plana
- Seja a parte da fronteira de que está contida na circunferência de equação e a parte da fronteira de que está contida na circunferência de equação . Descreva e nos seguintes formatos:
- Descreva a região plana utilizando coordenadas polares, no seguinte formato:
- Calcule a integral dupla utilizando o método que preferir.
Explicitando as constante , , e e as funções e
Explicitando as funções e e as constantes e
Questão 81
Calcule , em que é a região acima do eixo e dentro da circunferência . Esboce a região de integração.
Ver solução completaQuestão 84
Utilizando coordenadas polares calcule a integral dupla em que é a região plana, no primeiro quadrante, limitada pelas retas e pela circunferência
Ver solução completaQuestão 85
Calcule a seguinte integral
Em que é a região limitada pelas retas e e pela circunferência , no terceiro quadrante
Ver solução completaQuestão 86
Usando coordenadas polares calcule a integral dupla
Em que é a região no primeiro quadrante no plano , acima da reta e abaixo da circunferência
Ver solução completaQuestão 88
Calcule a seguinte integral
Em que é a região do plano limitada pelo semicírculo e o eixo
Ver solução completaQuestão 89
Calcule a seguinte integral
Em que é a região do primeiro quadrante limitada pelo círculo e pelas retas e
Ver solução completaQuestão 91
2. Resolva as integrais duplas utilizando coordenadas polares:
a) em que é a parte do disco que está no primeiro quadrante e acima da reta .
Ver solução completaQuestão 93
Qual das alternativas abaixo exibe o valor correto da integral
Escolha uma:
a)
b)
c)
d)
e)
Ver solução completaQuestão 94
Calcule as integrais:
b) , onde é a região do primeiro quadrante limitada pelas circunferências e .
Ver solução completaQuestão 95
Calcule as integrais:
d) , onde é a região limitada pelas espiras e , com .
Ver solução completaQuestão 96
Calcule as integrais:
e) , onde é a região limitada pelo semicírculo e o eixo .
Ver solução completaQuestão 97
Calcule as integrais:
c) , onde é a região interior à cardioide e exterior à circunferência .
Ver solução completaQuestão 99
Questão 1: Calcule a integral
Onde é a região limitada pela desigualdade .
Ver solução completaQuestão 100
(Cap 15.1 - Ex15) Utilize uma calculadora programável ou computador (ou o comando de soma de um SCA) para estimar
onde . Utilize a Regra do Ponto Médio com os seguintes números de quadrados de tamanhos iguais: e .
Ver solução completaQuestão 101
1. Seja a região limitada pelas curvas , , e . Mude a integral para coordenadas polares.
Ver solução completaQuestão 109
Considere a região do plano acima da reta dentro do círculo .
- Escreva em integrais iteradas em coordenadas cartesianas e em coordenadas polares.
- Escolha uma das formas encontradas no item anterior para mostrar que .
Questão 110
Seja o domínio representado na figura, onde é a parte da circunferência , é a parte da circunferência , é a parte da circunferência . Reescrever a integral dupla
na forma iterada:
3. usando coordenadas polares.
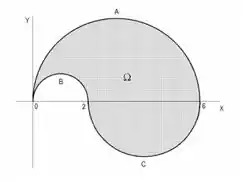
Questão 111
(Cap 15.1 - Ex13) Calcule a integral dupla, identificando-a antes com o volume de um sólido.
Ver solução completaQuestão 112
Questão 1: Expresse a área do domínio plano dado pelas relações abaixo como uma integral envolvendo coordenadas polares:
Ver solução completaQuestão 113
3) Calcule o valor da integral
Onde é a região delimitada pelas curvas e .
Ver solução completaQuestão 114
Questão 1: Sejam dois números reais positivos. Calcule a integral dupla , onde
Ver solução completaQuestão 116
Seja
- Transforme em uma só integral iterada na ordem invertida.
- Calcule para
Questão 117
Seja uma lâmina delgada representada pela região , determinada por , , e . Se a densidade em cada ponto é dada por , determine a massa de
Ver solução completaQuestão 120
Utilize as coordenadas polares para determinar o volume do sólido dado.
a) Abaixo do paraboloide e acima do disco
Ver solução completaQuestão 121
Utilize as coordenadas polares para determinar o volume do sólido dado.
b) Dentro da esfera e a fora do cilindro
Ver solução completaQuestão 123
Calcule o momento de Inercia com relação a origem de , onde e a função densidade
Ver solução completaQuestão 125
Considere a integral dupla em coordenadas polares:
a) Esboce a região de integração no plano cartesiano.
Sugestão: Analise a imagem das retas .
b) Calcule e interprete geometricamente a integral .
Ver solução completaQuestão 126
Exercício 1. Por meio de coordenadas polares, calcule a integral
(a) , em que é a região limitada pelo círculo .
Ver solução completaQuestão 127
Exercício 1. Por meio de coordenadas polares, calcule a integral
(b) , em que é a região anular limitada por e , .
Ver solução completa