Utilize a integral dupla para determinar a área da região.

A região interior a ambos os círculos e .

Vamos começar determinando a expressão do circulo em relação a e . Isso vai facilitar a construção do gráfico.

Vamos começar por:

Multiplicando os dois lados da expressão por , vamos ter:

Agora vamos ter que substituir na equação geral do círculo:

Substituindo, temos:

Porem sabemos que as relações de e com e são:

Podemos reescrever a equação do círculo, ficando com:

Agora devemos passa o para o outro lado e completar quadrado. Fazendo isso vamos ter:

Repare que podemos escrever a expressão da seguinte forma:

Essa expressão é exatamente uma circunferência com centro em e raio igual a .

Exatamente as mesmas etapas do passo 2, teremos que fazer para o círculo:

Na etapa anterior, fizemos um passo a passo, e aqui será exatamente o mesmo processo. Para não ficar tão repetitivo e igual as etapas anteriores, vamos avançar algumas das etapas aqui. Certo?

Sabemos que temos que multiplicar os dois lados por, e substituir na expressão geral do círculo. Fazendo isso temos:

Sabemos também que:

Então, vamos substituir na expressão acima e completar quadrados, para então encontrar a expressão do círculo. Fazendo isso temos que:

Passando para o outro lado e completando quadrados, temos:

Logo, simplificando vamos ter:

Repare que a expressão é exatamente uma circunferência com centro em e raio igual a .

Agora podemos fazer um esboço dessas curvas. Vamos utilizar o Geogebra para ter uma precisão e ficar claro a região a ser avaliada.

Mas observe as expressões que facilmente você faz esses esboços a mão. Ambos os círculos tem raio igual a , a diferença que um deles está com a origem sobre o eixo em , e o outro sobre o eixo em .

Vamos plotar as duas expressões:

Temos que:

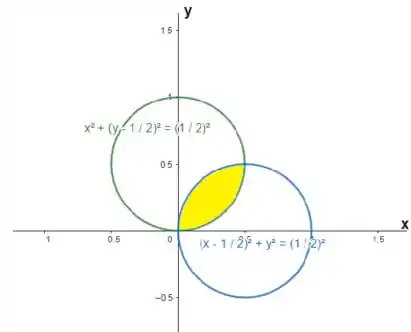
Precisamos determinar os pontos de encontro entre as curvas.

Já sabemos que um ponto é na origem, e para determinar o outro basta igularamos as expressões polares:

Dessa forma:

Para qual ângulo no primeiro quadrante, o seno e cosseno serão iguais. Isso acontece apenas para um ângulo, que é:

Logo podemos concluir que a variação do ângulo é:

Agora vamos usar um macete para facilitar nossa vida. Observe que se traçarmos uma reta ela vai passar exatamente pelos pontos de intersecção:

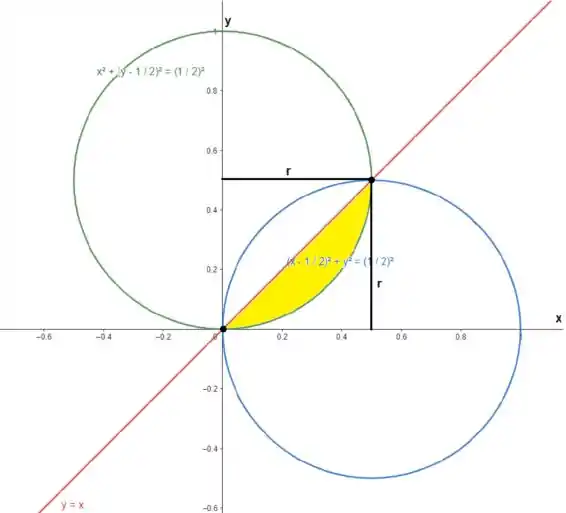
Isso ocorre, devido a simetria dos círculos. Isso vai facilitar nossa vida, porque podemos achar a área da região em amarelo acima e multiplicar por .

A expressão em coordenadas polares da figura em verde é:

Dessa forma temos que:

Nossa integral tem essa cara, certo:

Em coordenadas polares, fica:

Substituindo os limites de integração e também multiplicando por dois, pois estamos calculando apenas metade da área, vamos ter:

Agora devemos resolver a integral. Lembrando que começamos integrando de dentro para fora.

Integrando em , temos:

Aplicando os limites de integração temos que:

Vamos utilizar uma relação trigonométrica da seguinte forma:

Substituindo, vamos ter:

Podemos separar essa integral da seguinte forma:

Aqui vamos precisar fazer uma substituição do tipo:

Substituindo, temos:

Integrando e voltando para a variável , temos:

Aplicando os limites de integração, vamos ter:

Simplificando, nossa resposta é: