Faça o gráfico das duas soluções básicas da equação diferencial e de várias outras soluções. Que aspecto têm em comum as suas soluções?

16-

A cara da solução quando temos raízes complexas é igual a:

Logo a solução será igual a:

O link que vai nos auxiliar para conseguirmos ver o comportamento dessa função é:

https://www.desmos.com/calculator/8bonyqgqze

E o gráfico pode ser visto aqui:

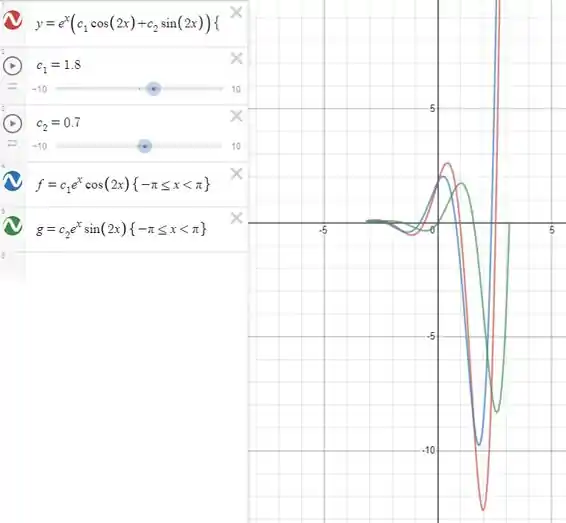
Os gráficos tem essa característica oscilatória e para temos uma divergência e para