Enunciado
Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 6.1 - Ex. 34
34. Ache o volume d sólido gerado pela otação, emtorno do eixo x, da região limitaa pelo laço da curva cuja equação é
Passo 1
de tudo, vamos esboçar o laço dessa curva rotacionadas em relação ao eixo x:
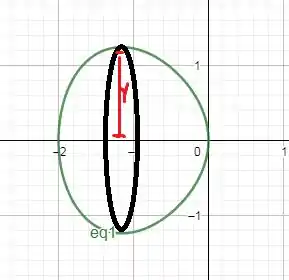
x varia entre -2 a 0.
o raio dessa figura rotacionada seria dado por
Lembrando que a fórmula do volume é dada por
Passo 2
A integral ficará assim:
Lembrando que x está variando de -1/2 a 1, por isso que esses são os limites da integral.
Substituindo,
Pronto, agora é só continha, Fazendo o mmc
Resposta
Exercícios de Livros Relacionados
Encontre o volume do sólido obtido pela rotação da região limitada pelas curvas dadas em torno das retas especificadas. Esboce a região, o sólido e um disco ou arruela típicos y = x - 1 ,x = 5 ,y = 0
Encontre o volume do sólido obtido girando a região delimitada pelas curvas dadas sobre a linha especificada. Esboce a região, o sólido e um disco ou arruela típico. y = 1 / x ,y = 0 , x = 1 , x = 4 ;
Encontre o volume do sólido obtido pela rotação da região limitada pelas curvas dadas em torno das retas especificadas. Esboce a região, o sólido e um disco ou arruela típicos y = 25 - x 2 ,y = 0 ,x =
Encontre o volume do sólido obtido girando a região delimitada pelas curvas dadas sobre a linha especificada. Esboce a região, o sólido e um disco ou arruela típico. y = 6 - x 2 ,y = 2 s o b r eoe i x
Encontre o volume do sólido obtido girando a região delimitada pelas curvas dadas sobre a linha especificada. Esboce a região, o sólido e um disco ou arruela típico. y = x 3 , y = 0 ,x = 1 ; s o b r e