Enunciado
Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 6.1 - Ex. 40
40. A região no primeiro quadrante, limitada pelos eixos coordenados, pela reta y=1 e pelas curva faz uma rotação em torno do eixo x. Ache o volume do sólido gerado.
Passo 1
Antes de tudo, vamos esboçar essas curvas,
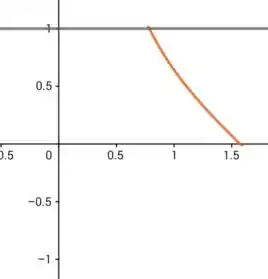
Rotacionado-as em torno do eixo x, temos
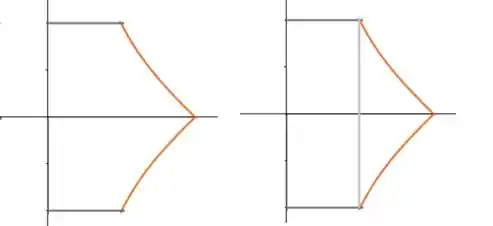
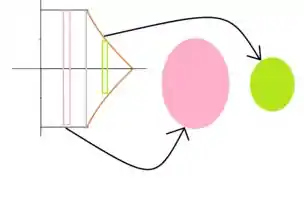
Antes de começarmos as nossas continhas, é necessário fazer um corte circular na figura, formando assim um disco. Se liga nas ilustrações:
Passo 2
Para o disco rosa, sua área é
Para o disco verde,
Passo 3
A integral ficará assim:
x está variando de 0 até na primeira integral, para chegar nessa mesma conclusão basta igualar as curvas.
Além disso, a curva toca no eixo x quando , por isso que na segunda integral está variando de .
Substituindo :
Para resolver a segunda integral, usaremos uma relação trigonométrica:
Resolvendo essas continhas, encontraremos que o volume é