Enunciado
Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 2.5 - Ex. 34
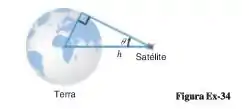
34-Um satélite de observação pode ver somente uma parte da superfície da Terra. Ele tem sensores de horizonte que permitem calcular o ângulo , o qual pode ser visto na figura abaixo. Suponha que a Terra (esférica) tenha um raio e que a distância do satélite a partir da superfície dela seja .
a)Mostre que
b) Considerando e supondo que o satélite se aproxime da Terra, encontre a taxa segundo a qual está variando em relação a quando . Expresse sua resposta em quilômetro/grau.
Passo 1
a)Galerinha, nós temos que:
Assim,
Fácil, né ?
Passo 2
b)Nesse item nós só vamos derivar:
Resposta
a)Demonstração acima.
b)A taxa é igual a zero.
Exercícios de Livros Relacionados
Um fio com B metros de comprimento é cortado em duas partes. Uma parte é dobrada para formar um triangulo equilátero e a outra para forma um circulo. Se a soma das áreas delimitadas por cada parte for
Determine a fórmula para a derivada em relação a x de sec x c o s s e cx c o t gx
Determine a fórmula para a derivada em relação a x de sec x c o s s e cx c o t gx
Represente graficamente y = cos x para - π ≤ x ≤ 2 π . Na mesma tela, esboce o gráfico y = s e n x + h - s e n ( x ) h Para h = 1 ; 0.5 ; 0.3 ; 0.1 . Então, em uma nova janela, tente h = - 1 ; - 0.5
Represente graficamente y = - sen x para - π ≤ x ≤ 2 π . Na mesma tela, esboce o gráfico y = cos x + h - cos x h Para h = 1 ; 0.5 ; 0.3 ; 0.1 . Então, em uma nova janela, tente h = - 1 ; - 0.5 e