Enunciado
Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 9.1 - Ex. 36
36)
Ache o volume do solido gerado pela rotação da região do exercício 35 em torno do eixo x.
Passo 1
Entendendo o problema
- A região é mostrada na figura 1, se fazemos uma rotação em x obteremos um
- Suponhamos uma fatia daquela área note que, ao gira essa fatia fira um disco com raio igual ln x. Usando a formula da área do circulo; A(x) = , o volume encontramos integrando a área não é?
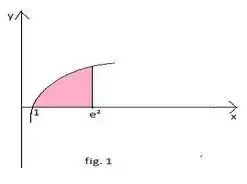
solido como mostrado na figura 2.
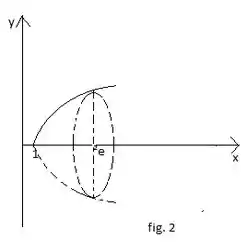
Passo 2
, certo?
Usando integração por partes;
Seja f(x) = ln²x derivando f’(x) = 2
g’(x) = 1 integrando g(x) = x
Substituindo na formula ficamos com;
= x.ln x -
= x.ln x- 2
Note que devemos usar novamente interação por partes;
Seja f(x) = l derivando f’(x) =
g’(x) = 1 integrando g(x) = x
Substituindo na formula temos;
=
=,
Substituindo na expressão original temos;
Passo 3
=
=
=
Logo;
=
= 2( e²-1)
Resposta
= 2( e²-1).
Exercícios de Livros Relacionados
Calcule o volume do sólido obtido pela rotação, em torno do eixo x, do conjunto de todos os pares ( x , y ) tais quee) y ≥ 0 ,1 ≤ x ≤ 2ex 2 - y 2 ≥ 1 .
Calcule o volume do sólido obtido pela rotação, em torno do eixo x, do conjunto de todos os pares ( x , y ) tais queh) 0 ≤ y ≤ xex 2 + y 2 ≤ 2 .
Calcule o volume do sólido obtido pela rotação, em torno do eixo x, do conjunto de todos os pares ( x , y ) tais quef) 0 ≤ x ≤ 1ex ≤ y ≤ 3 .
Calcule o volume do sólido obtido pela rotação, em torno do eixo x, do conjunto de todos os pares ( x , y ) tais quej) 1 ≤ x 2 + y 2 ≤ 4ey ≥ 0 .
Calcule o volume do sólido obtido pela rotação, em torno do eixo x, do conjunto de todos os pares ( x , y ) tais quec) 1 ≤ x ≤ 4e0 ≤ y ≤ x