Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Um curso de Cálculo Volume 2 - 5ª Edição - Hamilton Luiz Guidorizzi- Ed: 5º - Capítulo 3.1 - Ex. 1h

  1. Calcule o volume do sólido obtido pela rotação, em torno do eixo x, do conjunto de todos os pares ( x , y ) tais que

h) 0 ≤ y ≤ x   e   x 2 + y 2 ≤ 2 .

Passo 1

Fórmula para o volume do sólido,

V = π ∫ a b f x 2 d x

Passo 2

Aplicando em nossa questão:

Para   x 2 + y 2 ≤ 2   e   0 ≤ y ≤ x , são as curvas   y = x   e circunferência de raio   2 , com a rotação e delimitada por   0 ≤ x ≤ 2 , o gráfico será dessa forma:

  V 1 = π ∫ 1 2 2 - x 2 2 d x

  V 2 = π ∫ 0 1 x 2 d x

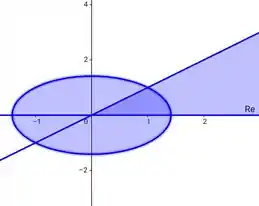
Passo 3

Resolvendo...

V 1 + V 2 = π 2 x - x 3 3 | 1 2 + π x 3 3 | 0 1 = π 2 2 - 2 2 3 - 2 + 1 3 + 1 3 = π 6 2 3 - 2 2 3 - 6 3 + 2 3 = π 4 2 3 - 4 3 = 4 π 3 2 - 1

Resposta

  V = 4 π 3 2 - 1

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

8. x = y^2 + 1 , x = (1)/(2) , y = - 2 e y = 2
Determinar o volume do sólido de revolução gerado pela rotação, em torno do eixo dos x, da região R delimitada pelos gráficos das equações dadas. y = x 2ey = x 3
Determinar o volume do sólido de revolução gerado pela rotação, em torno do eixo dos x, da região R delimitada pelos gráficos das equações dadas. y = x + 1 ,x = 2ey = 0
Determinar o volume do sólido de revolução gerado pela rotação, em torno do eixo dos x, da região R delimitada pelos gráficos das equações dadas. y = x 2 + 1 ,x = 0 ,x = 2ey = 0
Considere a região englobada por y = arcsinh ⁡ x , y = 0 e x = 1 . Monte, mas não calcule , uma integral que represente o volume do sólido obtido quando a região gira em torno do eixo x usando(a) disc