Enunciado
Cálculo - Cálculo Volume 1 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 3.1 - Ex. 38
37-38 Estime o valor de dando um zoom no gráfico de . Depois derive a e determine o valor exato de e compare com a sua estimativa.
37.
Passo 1
Olá, meu querido aluno. Vamos resolver juntos essa atividade.
Aqui a gente precisa encontrar a derivada da função:
No ponto , de duas formas. Uma utilizando métodos gráficos, e a outra forma é calculando a derivada da forma que estamos acostumados.
Lembre-se do seu início estudando derivadas, onde a derivada da função no ponto dado é a reta tangente nesse ponto.
Então para calcularmos a derivada dessa forma, devemos traçar uma reta tangente na função, em , onde essa reta será a hipotenusa de um triangulo que iremos criar, a partir desse triangulo iremos calcular a inclinação dessa reta com o cateto adjacente, e assim teremos nossa derivada.
Passo 2
Faremos primeiramente o gráfico de , com o ponto em :
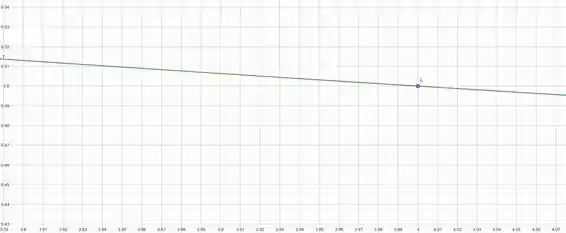
Agora iremos adicionar dois pontos, que irão nos ajudar a completarmos o triangulo que queremos:
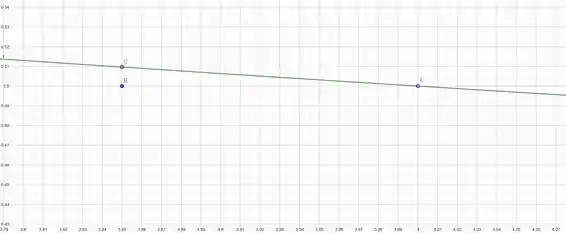
As coordenadas dos pontos, são:
E o triangulo é:
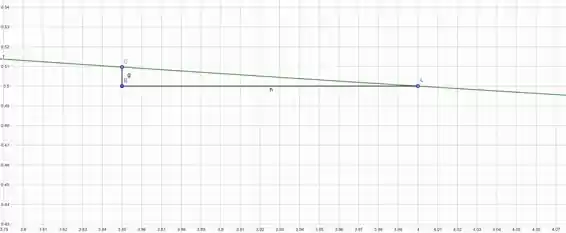
Agora calculando o ângulo:
Veja que em queremos a altura, sendo assim iremos trabalhar com as coordenadas , já em iremos trabalhar com as coordenadas :
É aproximado, pois não conseguiríamos traçar certinha a reta!
Passo 3
Agora faremos a derivada de .
Vamos reescrever a divisão e a raiz:
Vamos aplicar a regra de derivação para polinômios:
Temos então a nossa derivada:
Passo 4
Agora substituirmos o valor de para acharmos o valor de .
Supomos o valor de e achamos o valor real de . São bem parecidos hein!!!