Enunciado
Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 3.Exercícios Práticos - Ex. 106
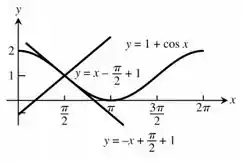
Encontre equações para a tangente e para a normal à curva no ponto .
Esboce a curva, a tangente e a normal juntas, identificando cada uma com a sua respectiva equação.
Passo 1
Para achar a equação da reta tangente usamos , onde é o coeficiente angular da reta e é igual a primeira derivada da função naquele ponto e depois substituímos o ponto nesta equação. Para achar a equação da reta normal utilizamos que o produto dos coeficientes angulares de duas retas normais é igual a . Para esboçar o gráfico tomamos o gráfico de e deslocamos para cima de 1 unidade e em seguida desenhamos a reta tangente no ponto dado e uma reta normal.
Passo 2
No ponto :
Substituindo na equação da reta, temos:
Como a reta passa pelo ponto , substituímos esse ponto para achar :
Passo 3
Precisamos achar agora a equação da reta normal:
E temos:
Como a reta passa pelo ponto , substituímos esse ponto para achar :
Resposta
