Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 6.6 - Ex. 38

38 - Use os teoremas de Pappus para determinar a área de superfície lateral e o volume e de um cone circular reto.

Passo 1

Primeiramente vamos criar um cone de coordenadas ( 0,0 ) ( h , r ) ( h , 0 ) sobre o eixo x, e obteremos uma imagem conforme a mostrada abaixo:

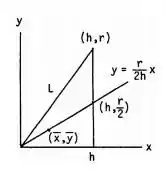
Assim o cone terá altura h e raio r.

Logo: S = 2 π y - L

Assim:

S = 2 π r 2 h 2 + r 2 = π r h 2 + r 2

Para calcularmos o volume precisaremos saber a distância da centroid do triângulo:

y = r 2 h x

Pela coordenada x, precisaremos utilizar a fórmula:

x - h 2 + r 2 h x - r 2 2 = 1 3 h 2 + r 2 4

Assim:

4 h 2 + r 2 4 h 2 x 2 - 4 h 2 + r 2 2 h x + r 2 4 + 2 r 2 + 4 h 2 9 = 0

Resolva utilizando a fórmula da equação do segundo grau e obtenha:

x 1 = 2 h 3 e   x 2 = 4 h 3 ⇒ x - = 2 h 3

Pelo teorema de Pappus:

V = 2 π r 3 1 2 h r = π h r 2 3

Resposta

V =   π h r 2 3

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Encontre a área exata da superfície obtida girando a curva em torno do eixo x. 7 .y = x 3 ,0 ≤ x ≤ 2
Calcule a área da superfície obtida pela rotação da curva em torno do eixo x . y = 1 + 4 x ,1 ≤ x ≤ 5
(a) Configure uma integral para a área da superfície obtida por girar a curva em torno de (i) o eixo x e (ii) o eixo y . 6 .y = tan - 1 ⁡ x ,0 ≤ x ≤ 2
Calcule a área da superfície obtida pela rotação da curva em torno do eixo x . 9 x = y 2 + 18 ,2 ≤ x ≤ 6
Encontre a área exata da superfície obtida pela rotação da curva em torno do eixo x : x = 1 3 y 2 + 2 3 / 2 ,1 ≤ y ≤ 2