Enunciado
Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 3.2 - Ex. 40
40. Um fabricante pode obter um lucro de 20 dólares em cada item se até 800 itens forem produzidos por semana. O lucro decresce 0,02 dólares por item acima de 800. (a) Se x itens forem produzidos por semana, expresse o lucro do fabricante como uma função de x. (b) Como x é o número de itens, é um inteiro não negativo. Para que tenhamos as exigências de continuidade do cálciilo, x deve ser um número real não negativo. Com essa hipótese, mostre que a função da parte (a) é contínua até 800, mas não derivável nesse número.
Passo 1
Primeira coisa que devemos fazer antes de iniciar está questão é encontrar a função que modela o problema de acordo com as informações contidas no enunciado, que exatamente o que ele nos pede na letra (a). Uma outra coisa também que devemos perceber logo de cara é que essa função se trata de uma função definida por partes, pois ela muda seu comportamento a partir de uma certa quantidade x de itens produzidos.
Passo 2
Letra (a)
Assim reunindo as informações contidas no enunciado, podemos afirmar que a função que expressa o lucro do fabricante será dada por
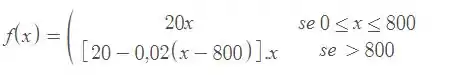
Passo 3
Letra (b)
Para determinar se f(x) é continua em um ponto deve-se atender a 3 pré-requisitos, ou seja , para uma função ser continua em x0:
f(x0) tem que existir;
-
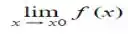tem que existir; -
.
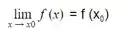Assim, deve-se verificar cada um dos itens ácima para dizer se f(x) é continua em x0.
Passo 4
Ao substituir x0 = 800 na função, percebemos que a expressão onde vamos substituir esse valor é a primeira função, pois a mesma está definida para x0 = 800. Com isso temos que
f ( 800 ) = 16000.
Passo 5
Para verificar que um limite existe devemos lembrar do conceito de limites laterais, ou seja , 
.
Assim, temos que :
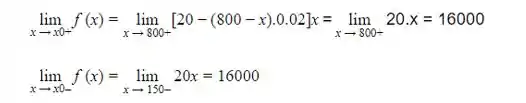
Com isso podemos afimar que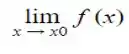 
existe e é igual a 16000.
Passo 6
Verificando a ultima condição , temos:
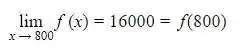
Com isso, como os 3 itens necessários foram atendidos; pode-se afirmar que f (x) é continua em x0 = 800.
Passo 7
Uma função f definida num intervalo aberto que contém x1 será derivável em x1 se e somente se 
ambas existirem e forem iguais.
A derivada à esquerda de f em x1, denotada por f’ - (x1), será definda por
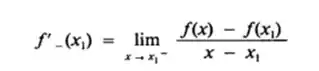
A derivada à direita de f em x1, denotada por f’ + (x1), será definda por
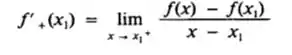
Passo 8
A derivada à esquerda de f(X) em x1 = 800 será:
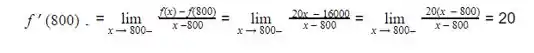
Passo 9
A derivada à direita de f(X) em x1 = 150 será :
Passo 10
Como obtemos que 
não existe. Assim, f(X) não é derivável em x1 = 800. Com isso, percebe-se que uma função ser contínua em X1 , não necessariamente implica que ela é derivável em X1.
Resposta
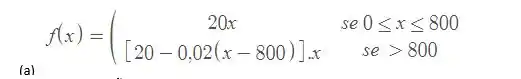
Demonstração.